Giải bài tập SGK Toán 8 Bài 12: Hình vuông

a) Một hình vuông có cạnh bằng \(3cm\). Đường chéo của hình vuông đó bằng \(6cm\),  \(\sqrt{18}cm\), \(5cm\) hay \(4cm\)?

b) Đường chéo của một hình vuông bằng \(2dm\). Cạnh của hình vuông đó bằng: \(1dm, \dfrac{3}{2}dm\), \(\sqrt{2}dm\) hay \(\dfrac{4}{3}dm\)?

Phương pháp giải

Áp dụng định lí Pytago: Bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

Hướng dẫn giải

Câu a

Ta có: \({a^{2}} = {\rm{ }}{3^2} + {\rm{ }}{3^2} = {\rm{ }}18\) (định lí Pytago)

Suy ra \(a = \sqrt{18}\) (cm)

Vậy đường chéo của hình vuông cạnh \(3\,cm\) là \(\sqrt{18}cm\).

Câu b

Gọi cạnh của hình vuông là \(a\).

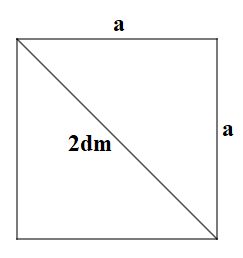
Áp dụng định lí Pytago ta có

Ta có  \({a^2} + {a^2} = {2^2} \Rightarrow 2{a^2} = 4 \Rightarrow {a^2} = 2\)\( \Rightarrow a = \sqrt{2}\)

Vậy cạnh của hình vuông có đường chéo \(2\,dm\) là \(\sqrt{2}dm\).

Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.

Phương pháp giải

Áp dụng

• Hình bình hành nhận giao điểm của hai đường chéo là tâm đối xứng.
• Hình thang cân nhận đường thẳng nối trung điểm hai cạnh đáy là trục đối xứng.
• Hình thoi nhận hai đường chéo là hai trục đối xứng. 

Hướng dẫn giải

Hình vuông cũng là hình bình hành nên nhận O là giao điểm của hai đường chéo là tâm đối xứng.

Hình vuông cũng là hình thoi nên nhận hai đường chéo AC và BD là các trục đối xứng.

Hình vuông cũng là hình thang cân nên nhận đường thẳng nối trung điểm các cặp cạnh đối diện là trục đối xứng.

Vậy hình vuông có 1 tâm đối xứng và 4 trục đối xứng như trên.

Cho hình 106. Tứ giác AEDF là hình gì? Vì sao?

Phương pháp giải

Áp dụng dấu hiệu nhận biết hình vuông: Hình thoi có một góc vuông là hình vuông.

Hướng dẫn giải

Tứ giác \(AEDF\) có \(EA // DF\) (cùng vuông góc \(AC\)) 

\(DE // FA\) (cùng vuông góc với \(AB\))

Suy ra \(AEDF\) là hình bình hành (dấu hiệu nhận biết hình bình hành)

Hình bình hành \(AEDF\) có đường chéo \(AD\) là phân giác của góc \(A\) (giả thiết) nên là hình thoi (dấu hiệu nhận biết hình thoi)

Hình thoi \(AEDF\) có \(\widehat {EAF} = \widehat {EAD} + \widehat {DAF} = {45^0} + {45^0} \)\(= {90^0}\)

\(\Rightarrow \) Hình thoi \(AEDF\) có \(1\) góc vuông nên là hình vuông (dấu hiệu nhận biết hình vuông)

Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông.

Phương pháp giải

Áp dụng

• Dấu hiệu nhận biết hình thoi: Tứ giác có \(4\) cạnh bằng nhau là hình thoi.
• Dấu hiệu nhận biết hình vuông: Hình thoi có một góc vuông là hình vuông.

Hướng dẫn giải

Các tam giác vuông \(AEH, BFE, CGF, DHG\) có

\(AE = BF = CG = DH\) (1) (giả thiết)

Theo giả thiết \(ABCD\) là hình vuông nên \(AB=BC=CD=DA\)  (2) (tính chất hình vuông)

Mà: \(AH = AD - DH, BE = AB - AE, \)\(CF = BC - BF, DG = DC - CG \) (3)

Từ (1), (2) và (3) suy ra \(AH = BE = CF = DG\)

Suy ra \(∆AEH =  ∆BFE =  ∆CGF \)\(=  ∆DHG\) (hai cạnh góc vuông)

Do đó

\(\widehat{EHA} = \widehat{FEB}\) (4) (hai góc tương ứng bằng nhau)

\(HE = EF = FG = GH\) ( các cạnh tương ứng)    

 \( \Rightarrow \) Tứ giác \(EFGH\) là hình thoi (dấu hiệu nhận biết hình thoi)             

Xét tam giác \(AHE\) vuông tại \(A\) nên \(\widehat{HEA}\) + \(\widehat{EHA}=90^0\)   (5)

Ta có

\(\widehat{HEF} + \widehat{HEA}\)\(+ \widehat{FEB}= 180^0 \)

Kết hợp với (4) và (5), ta có:

\(\widehat{HEF} = 180^0- (\widehat{HEA}\) + \(\widehat{FEB}) \)

\(= 180^0- (\widehat{HEA}\) + \(\widehat{EHA})\)

\(= 180^0- 90^0= 90^0\)

\( \Rightarrow \) Hình thoi \(EFGH\) là hình vuông (dấu hiệu nhận biết hình vuông)

Các câu sau đúng hay sai?

a) Tứ giác có hai đường chéo vuông góc với nhau là hình thoi.

b) Tứ giác có hai đường chéo vuông góc nhau tại trung điểm của mỗi đường là hình thoi.

c) Hình thoi là tứ giác có tất cả các cạnh bằng nhau.

d) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.

e) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

Phương pháp giải

Áp dụng: Các dấu hiệu nhận biết hình thoi, hình vuông.

Hướng dẫn giải

Câu a: Sai vì tứ giác phải có đủ điều kiện hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.

Câu b: Đúng (dấu hiệu nhận biết hình thoi)

Câu c: Đúng (dấu hiệu nhận biết hình thoi)

Câu d: Sai vì khi đó chưa chắc các cạnh của hình chữ nhật bằng nhau nên chưa thể kết luận là hình vuông.

Câu e: Đúng (dấu hiệu nhận biết hình vuông)

Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.

a) Tứ giác AEDF là hình gi? Vì sao?

b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông?

Phương pháp giải

Áp dụng dấu hiệu nhận biết

• Hình bình hành có các cạnh đối song song,
• Hình bình hành có một đường chéo là tia phân giác của một góc là hình thoi,
• Hình bình hành có một góc vuông là hình chữ nhật,
• Hình thoi có một góc vuông là hình vuông.

Hướng dẫn giải

Câu a: Xét tứ giác \(AEDF\) có

 \(DE // AF, DF // AE\) (giả thiết)

\( \Rightarrow \)  Tứ giác \(AEDF\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

Câu b: Hình bình hành \(AEDF\) là hình thoi thì \(AD\) là tia phân giác của \(\widehat {CAB}\).

Do đó \(D\) là giao điểm của tia phân giác của \(\widehat {CAB}\) với \(BC\) thì hình bình hành \(AEDF\) là hình thoi (dấu hiệu nhận biết hình thoi).

Câu c: Nếu  \(∆ABC\) vuông tại \(A\) thì hình bình hành \(AEDF\) có một góc vuông do đó hình bình hành \(AEDF\) là hình chữ nhật ( theo dấu hiệu nhận biết hình chữ nhật) 

Nếu \(∆ABC\) vuông tại \(A\) và \(D\) là giao điểm của tia phân giác của \(\widehat {CAB}\) với cạnh \(BC\) thì \(AEDF\) là hình vuông (vì khi đó \(AEDF\) là hình thoi có một góc vuông).

Cho hình chữ nhật ABCD có AB = 2AD.  Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE.

a) Tứ giác ADFE là hình gì? Vì sao?

b) Tứ giác EMFN là hình gì? Vì sao?

Phương pháp giải

Áp dụng dấu hiệu nhận biết:

• Tứ giác có một cặp cạnh đối song song và bằng nhau là hình bình hành,
• Tứ giác có các cặp cạnh đối song song là hình bình hành,
• Hình bình hành có một góc vuông là hình chữ nhật,
• Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

Hướng dẫn giải

Vì \(ABCD\) là hình chữ nhật nên \(AB=CD,AD=BC, AB//CD\)

Lại có \(E, F\) theo thứ tự là trung điểm của \(AB, CD\) nên \(AE=EB=\dfrac{AB}2\), \(DF=FC=\dfrac{DC}2\)

Lại có \(AB=2AD\) 

Suy ra \(AE = EB = BC = CF = FD = DA\)

Câu a: Xét tứ giác \(ADFE\) có

\(AE // DF\) (do \(AB//CD\)), \(AE = DF\) (chứng minh trên)

\( \Rightarrow \) Tứ giác \(ADFE\) là hình bình hành (dấu hiệu nhận biết hình bình hành)

Hình bình hành \(ADFE\) có \(\widehat{A} = 90^0\) nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật )

Hình chữ nhật \(ADFE\) có \(AE = AD\) (chứng minh trên) nên nó là hình vuông (dấu hiệu nhận biết hình vuông)

Câu b: Xét tứ giác \(DEBF\) có:

\(EB // DF\) (do \(AB//CD\)),  \(EB = DF\) (chứng minh trên)

\( \Rightarrow \) Tứ giác \(DEBF\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

\( \Rightarrow \) \(DE // BF\) (tính chất hình bình hành)

Xét tứ giác \(AECF\) có:

\(EA // CF\) (do \(AB//CD\)), \(EA = CF\) (chứng minh trên)

\( \Rightarrow \) Tứ giác \(AECF\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

\( \Rightarrow \) \(AF // EC\) (tính chất hình bình hành)

Xét tứ giác \(EMFN\) có: \(ME//NF,MF//NE\) (do \(DE // BF,AF//EC \) (chứng minh trên))

\( \Rightarrow \) Tứ giác \(EMFN\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

Theo câu a, \(ADFE\) là hình vuông nên \(ME = MF, ME  ⊥ MF\) (tính chất hình vuông)

Hình bình hành \(EMFN\) có \(\widehat{M} = 90^0\) nên là hình chữ nhật, lại có \(ME = MF\) nên là hình vuông (dấu hiệu nhận biết hình vuông)

Đố. Lấy một tờ giấy gấp làm tư rồi cắt chéo theo nhát cắt AB (h.108). Sau khi mở tờ giấy ra, ta được một tứ giác. Tứ giác nhận được là hình gì ? Vì sao ? Nếu ta có OA = OB thì tứ giác nhận được là hình gì ?

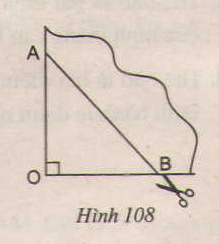
Phương pháp giải

Áp dụng

• Dấu hiệu nhận biết hình thoi: Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
• Dấu hiệu nhận biết hình vuông: Hình thoi có hai đường chéo bằng nhau là hình vuông.

Hướng dẫn giải

Tứ giác nhận được theo nhát cắt \(AB\) là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau (dấu hiệu nhận biết hình thoi).

Nếu có thêm \(OA = OB\) thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông (dấu hiệu nhận biết hình vuông).