Giải bài tập SGK Toán 8 Bài 7: Giải bài toán bằng cách lập phương trình (tiếp theo)

Lúc \(6\) giờ, một xe máy khởi hành từ A để đến B. Sau đó \(1\) giờ, một ô tô cũng xuất phát từ A đến B với vận tốc trung bình lớn hơn vận tốc trung bình của xe máy \(20km/h\). Cả hai xe đến B đồng thời vào lúc 9 giờ 30 phút cùng ngày. Tính độ dài quãng đường AB và vận tốc trung bình của xe máy?

Phương pháp giải

Bước 1: Đặt quãng đường AB là ẩn, tìm điều kiện của ẩn.

Bước 2: Biểu diễn các đại lượng còn lại theo ẩn đó.

Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình lập được.

Bước 4: Kết luận. (So sánh nghiệm tìm được với điều kiện của ẩn).

Hướng dẫn giải

Gọi \(x\) (km) là quãng đường AB \((x > 0)\).

Thời gian chuyển động từ A đến B của xe máy:

\(9\) giờ \(30\) phút - \(6\) giờ \(= 3\) giờ \(30\) phút \(=  \dfrac{7}{2}\) (giờ)

Vận tốc của xe máy là: \(x : \dfrac{7}{2} =  \dfrac{2x}{7}\) (km/h)

Ô tô xuất phát sau xe máy 1 giờ và đến B cùng lúc với xe máy 9 giờ 30 phút nên thời gian chuyển động từ A đến B của ô tô là: \( \dfrac{7}{2}- 1 =  \dfrac{5}{2}\) (giờ)

Vận tốc của ô tô là: \(x : \dfrac{5}{2} =  \dfrac{2x}{5}\) (km/h)

Vì vận tốc của ô tô hơn xe máy \(20km/h\) nên ta có phương trình:

\( \dfrac{2x}{5} -  \dfrac{2x}{7} = 20\)

\( \Leftrightarrow \dfrac{{7.2x}}{{35}} - \dfrac{{5.2x}}{{35}} = \dfrac{{20.35}}{{35}}\)

\(⇔ 14x - 10x = 700\)

\(⇔ 4x = 700\)

\( \Leftrightarrow x=700:4\)

\(⇔ x = 175\) (thỏa mãn)

Vậy quãng đường AB dài \(175\) km.

Vận tốc trung bình của xe máy: \(175 : \dfrac{7}{2} = 50\) (km/h). 

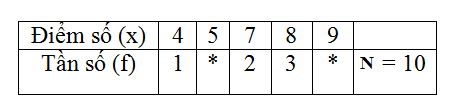
Điểm kiểm tra Toán của một tổ học tập được cho trong bảng sau:

Biết điểm trung bình của cả tổ là \(6,6\). Hãy điền các giá trị thích hợp vào hai ô còn trống (được đánh dấu *).

Phương pháp giải

Bước 1: Đặt số học sinh được điểm \(5\) là \(x\), tìm điều kiện của \(x\)

Bước 2:  Biểu diễn các đại lượng còn lại theo \(x\).

Bước 3:  Lập phương trình biểu diễn mối quan hệ giữa các đại lượng theo \(x\) và giải phương trình đó.

Bước 4:  Kết luận.

Hướng dẫn giải

Gọi \(x\) là số học sinh (tần số) được điểm \(5\) (\(0 < x < 10\); \(x\) nguyên)

Tần số của điểm \(9\) là: \(10 - (1 + 2 + 3 + x) = 4 - x\)

Điểm trung bình của cả tổ bằng \(6,6\) nên ta có phương trình:

\(\dfrac{{4.1 + 5x + 7.2 + 8.3 + 9.\left( {4 - x} \right)}}{{10}} \)\(\,= 6,6\)

\( \Leftrightarrow \dfrac{{4.1 + 5x + 7.2 + 8.3 + 9.\left( {4 - x} \right)}}{{10}}\)\(\, = \dfrac{{10.6,6}}{{10}}\)

\(⇔ 4 + 5x + 14 + 24 + 36 - 9x = 66\)

\(⇔ -4x + 78  = 66\)

\( \Leftrightarrow  - 4x = 66 - 78\)

\(⇔ -4x = -12\)

\( \Leftrightarrow x = \left( { - 12} \right):\left( { - 4} \right)\)

\(⇔ x = 3\) (thỏa mãn điều kiện)

Tần số của 9 là: \(4-x=4-3=1\)

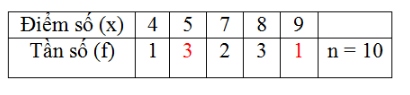
Vậy tần số của điểm \(5\) là \(3\) và tần số của điểm  \(9\) là \(1\).

Ta điền như sau: 

Lan mua hai loại hàng và phải trả tổng cộng \(120\) nghìn đồng, trong đó đã tính cả \(10\) nghìn đồng là thuế giá trị gia tăng (viết tắt VAT). Biết rằng thuế VAT đối với loại hàng thứ nhất là \(10\%\); thuế VAT đối với loại hàng thứ 2 là \(8\%\). Hỏi nếu không kể thuế VAT thì Lan phải trả mỗi loại hàng bao nhiêu tiền?

Phương pháp giải

Bước 1: Đặt tiền mua loại hàng thứ nhất không kể thuế VAT là \(x\),

Bước 2: Biểu diễn các đại lượng còn lại theo \(x\).

Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó.

Bước 4: Kết luận (Kiểm tra nghiệm tìm được với điều kiện)

Hướng dẫn giải

Tổng số tiền Lan phải trả khi mua hai loại hàng không kể thuế VAT là: 

\( 120000 - 10000 = 110000\) (đồng)

Gọi \(x\)(đồng) là tiền mua loại hàng thứ nhất không kể thuế VAT \((0 < x < 110000)\)

Tiền mua loại hàng thứ hai không kể thuế VAT: \(110000 - x\) (đồng)

Số tiền thực tế Lan đã trả cho loại hàng 1 là: \(x + 0,1x\) (đồng)

Số tiền thực tế Lan đã trả cho loại hàng 2 là: \(110000 - x + 0,08(110000 - x)\) (đồng)

Tổng số tiền thực tế Lan phải trả cho cả hai loại hàng là \(120000\) nên ta có phương trình:

\(x+ 0,1x + 110000 - x \)\(+ 0,08(110000 - x) = 120000\)

⇔\( 0,1x + 110000 + 8800 - 0,08x    \)\(= 120000\)

⇔ \(0,02x = 1200\)

\( \Leftrightarrow x = 1200:0,02\)

⇔ \(x = 60000\) (thỏa mãn)

Vậy số tiền trả cho loại hàng thứ nhất là \(60000\) đồng (không kể thuế VAT)

Số tiền phải trả cho loại hàng thứ hai không kể thuế VAT: \(110000-60000=50000\) đồng

Năm nay, tuổi mẹ gấp \(3\) lần tuổi Phương, Phương tính rằng \(13\) năm nữa thì tuổi mẹ chỉ còn gấp \(2\) lần tuổi Phương thôi. Hỏi năm nay Phương bao nhiêu tuổi?

Phương pháp giải

Bước 1: Đặt tuổi Phương hiện nay là \(x\), đặt điều kiện cho \(x\)

Bước 2: Biểu diễn các đại lượng còn lại theo \(x\).

Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình, tìm x.

Bước 4: Kết luận (Kiểm tra nghiệm tìm được có thỏa mãn điều kiện không).

Hướng dẫn giải

Gọi \(x\) là tuổi Phương hiện nay ( \(x\) nguyên dương)

Vì hiện nay tuổi mẹ gấp \(3\) lần tuổi Phương nên tuổi của mẹ hiện nay là: \(3x\) (tuổi)

Tuổi Phương \(13\) năm sau là: \(x + 13\) (tuổi)

Tuổi của mẹ \(13\) năm sau là: \(3x + 13\) (tuổi)

Vì \(13\) năm nữa thì tuổi mẹ chỉ còn gấp \(2\) lần tuổi Phương nên ta có phương trình:

\(3x + 13 = 2(x + 13)\)

\(⇔3x + 13 = 2x + 26\)

\( \Leftrightarrow 3x - 2x = 26 - 13\)

\(⇔x = 13\) (thỏa mãn điều kiện)

Vậy hiện nay Phương \(13\) tuổi.

Một số tự nhiên có hai chữ số. Chữ số hàng đơn vị gấp hai lần chữ số hàng chục. Nếu thêm chữ số \(1\) xen vào giữa hai chữ số ấy thì được một số mới lớn hơn số ban đầu là \(370\). Tìm số ban đầu.

Phương pháp giải

Bước 1: Đặt chữ số hàng chục là ẩn

Bước 2: Biểu diễn các đại lượng còn lại theo ẩn.

Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó. 

Bước 4: Kết luận

Hướng dẫn giải

Gọi \(x\) là chữ số hàng chục. (\(0 < x \le 9;x \in N)\)

Vì chữ số hàng đơn vị gấp hai lần chữ số hàng chục nên chữ số hàng đơn vị là: \(2x\)

Số tự nhiên lúc đầu là: \(\overline {x\left( {2x} \right)} \)

Số tự nhiên lúc sau là: \(\overline {x1\left( {2x} \right)} \)

Vì số mới hơn số ban đầu là \(370\) đơn vị nên ta có phương trình:

 \(\overline {x1\left( {2x} \right)}  - \overline {x\left( {2x} \right)}=370 \)

⇔\(\left( {100x + 10 + 2x} \right) - \left( {10x + 2x} \right) = 370\)

⇔\(100x + 10 + 2x - 10x - 2x = 370\)

⇔\(90x = 360\)

⇔\(x=360:90\)

⇔\(x = 4\) (thỏa mãn) 

Vậy chữ số hàng chục là \(4\) nên chữ số hàng đơn vị là: \(2.4 = 8\).

Do đó, số ban đầu là: \(48\).

*Lưu ý : Vì chỉ có 4 số có hai chữ số thỏa mãn điều kiện chữ số hàng đơn vị gấp đôi chữ số hàng chục là : 12 ; 24 ; 36 ; 48 nên ta có thể đi thử trực tiếp mà không cần giải bằng cách lập phương trình.

Tìm số tự nhiên có hai chữ số, biết rằng nếu viết thêm một chữ số \(2\) vào bên trái và một chữ số \(2\)  vào bên phải số đó thì ta được một số lớn gấp \(153\)  lần số ban đầu.

Phương pháp giải

Bước 1: Đặt số ban đầu là ẩn

Bước 2: Biểu diễn các đại lượng còn lại theo ẩn.

Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó.

Bước 4: Kết luận.

Hướng dẫn giải

Gọi số ban đầu là \(x\) (\(10 \le x \le 99\); \(x ∈\mathbb N)\)

Nếu viết thêm một chữ số \(2\) vào bên trái và một chữ số \(2\)  vào bên phải số đó thì ta được số mới là \(\overline {2x2} \) 

Vì \(x\) là số có hai chữ số nên \(\overline {2x2} \) là số có bốn chữ số do đó ta có thể tách như sau:

 \(\overline {2x2}= 2000 + 10x + 2 \) 

Vì số mới lớn gấp \(153\) lần số ban đầu nên ta có phương trình :

 \(\overline {2x2}  = 153x \)

\(\Leftrightarrow 2000 + 10x + 2 = 153x\) 

\( \Leftrightarrow 2000 + 2 = 153x - 10x\)

\(⇔2002 = 143x\)

\( \Leftrightarrow x=2002:143\)

\(⇔ x=14\) (thỏa mãn điều kiện)

Vậy số tự nhiên cần tìm là: \(14\).

Tìm phân số có đồng thời các tính chất sau:

a) Tử số của phân số là số tự nhiên có một chữ số;

b) Hiệu giữa tử số và mẫu số bằng \(4\);

c) Nếu giữ nguyên tử số và viết thêm vào bên phải của mẫu số một chữ số đúng bằng tử số, thì ta được một phân số bằng phân số \(\dfrac{1}{5}\).

Phương pháp giải

Bước 1: Đặt tử số của phân số cần tìm là ẩn

Bước 2: Biểu diễn các đại lượng còn lại theo ẩn.

Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó.

Bước 4: Kết luận (Kiểm tra xem nghiệm tìm được có thỏa mãn điều kiện của ẩn không).

Hướng dẫn giải

Gọi \(x\) là tử số của phân số cần tìm (\(0 < x \le 9)\); \(x ∈\mathbb N\)

Vì hiệu giữa tử số và mẫu số bằng \(4\) nên tử số lớn hơn mẫu số 4 đơn vị. Suy ra mẫu số của phân số đó là:\(x - 4\left( {x \ne 4} \right)\)

Nếu giữ nguyên tử số và viết thêm vào bên phải của mẫu số một chữ số đúng bằng tử số thì mẫu số mới là: \(\overline {\left( {x - 4} \right)x} \)

Nếu giữ nguyên tử số và viết thêm vào bên phải của mẫu số một chữ số đúng bằng tử số, thì ta được một phân số bằng phân số \(\dfrac{1}{5}\) nên ta có phương trình:

\(\dfrac{x}{{\overline {\left( {x - 4} \right)x} }} = \dfrac{1}{5}\)

\( \Leftrightarrow \dfrac{{5x}}{{5.\overline {\left( {x - 4} \right)x} }} = \dfrac{{\overline {\left( {x - 4} \right)x} }}{{5.\overline {\left( {x - 4} \right)x} }}\)

\(\Rightarrow 5x = {\overline {\left( {x - 4} \right)x}}\)

 \(⇔ 5x = 10\left( {x - 4} \right) + x\) 

 \(⇔5x = 10x - 40 + x\) 

 \( \Leftrightarrow 10x + x - 5x = 40\)

 \( \Leftrightarrow 6x = 40\)

 \( \Leftrightarrow x = 40:6\)

 \( \Leftrightarrow x = \dfrac{{20}}{3}\) (không thỏa mãn).

Vậy không có phân số thỏa mãn các yêu cầu của bài toán.

Điểm kiểm tra Toán của một lớp được cho trong bảng dưới đây:

trong đó có hai ô trống (thay bằng dấu *). Hãy điền số thích hợp vào ô trống, nếu điểm trung bình của lớp là 6,06

Phương pháp giải

Bước 1: Đặt tần số của điểm \(4\) là ẩn.

Bước 2: Biểu diễn các đại lượng còn lại theo ẩn.

Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó.

Bước 4: Kết luận (Kiểm tra nghiệm tìm được có thỏa mãn điều kiện không).

Hướng dẫn giải

Gọi x là tần số của điểm 4 (x nguyên dương)

Số học sinh của lớp là: \(2 + x + 10 + 12 + 7 + 6 + 4 + 1 = 42 + x\)

Vì điểm trung bình bằng 6,06 nên:

\(\frac{{2.3 + 4.x + 5.10 + 6.12 + 7.7 + 6.8 + 9.4 + 10.1}}{{42 + x}} = 6,06\)

Giải phương trình tìm được x=8 (thỏa)

Vậy ta có kết quả điền vào như sau:

Một xí nghiệp kí hợp đồng dệt một số tấm thảm len trong \(20\) ngày. Do cải tiến kỹ thuật, năng suất dệt của xí nghiệp đã tăng \(20\% \). Bởi vậy, chỉ trong \(18\) ngày, không những xí nghiệp đã hoàn thành số thảm cần dệt mà còn dệt thêm được \(24\) tấm nữa. Tính số tấm thảm len mà xí nghiệp phải dệt theo hợp đồng.

Phương pháp giải

Bước 1: Đặt số tấm thảm len mà xí nghiệp phải dệt theo hợp đồng là ẩn.

Bước 2: Biểu diễn các đại lượng còn lại theo ẩn.

Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó.

Bước 4: Kết luận.

Hướng dẫn giải

Gọi \(x\) là số tấm thảm len mà xí nghiệp phải dệt theo hợp đồng (\(x\) nguyên dương)

Số tấm thảm len mỗi ngày dự định dệt là: \(\dfrac{x}{{20}}\) (tấm)

Số tấm thảm len thực tế đã dệt là: \(x + 24\) (tấm)

Số tấm thảm len thực tế mỗi ngày dệt là: \(\dfrac{{x + 24}}{{18}}\) (tấm)

Vì năng suất của xí nghiệp tăng \(20\% \) nên số thảm thực tế dệt trong một ngày bằng \(100\%+20\%=120\% \) số thảm dự định  dệt trong một ngày, ta có phương trình: 

\(\eqalign{
& {{x + 24} \over {18}} = 120\% .{x \over {20}} \cr
& \Leftrightarrow {{x + 24} \over {18}} = {6 \over 5}.{x \over {20}} \cr
& \Leftrightarrow {{50\left( {x + 24} \right)} \over {900}} = {{9.6x} \over {900}} \cr
& \Leftrightarrow 50\left( {x + 24} \right) = 54x \cr
& \Leftrightarrow 50x + 1200 = 54x \cr
& \Leftrightarrow 1200 = 54x - 50x \cr
& \Leftrightarrow 4x = 1200 \cr
& \Leftrightarrow x = 1200:4 \cr
& \Leftrightarrow x = 300 \text{(thỏa mãn)}\cr} \)

Vậy số tấm thảm len xí nghiệp phải dệt theo hợp đồng là \(300\) tấm.

Một người lái ô tô dự định đi từ A đến B với vận tốc \(48 km/h\). Nhưng sau khi đi được một giờ với vận tốc ấy, ô tô bị tàu hỏa chắn đường trong \(10\) phút. Do đó, để kịp đến B đúng thời gian đã định, người đó phải tăng vận tốc thêm \(6 km/h\). Tính quãng đường AB.

Phương pháp giải

Bước 1: Đặt quãng đường AB là ẩn.

Bước 2: Biểu diễn các đại lượng còn lại theo ẩn.

Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó.

Bước 4: Kết luận.

Hướng dẫn giải

Gọi \(x\) là quãng đường AB \((x > 0; km)\)

Đổi: \(10\) phút = \( \dfrac{1}{6}\) giờ.

Đoạn đường ô tô đi trong \(1\) giờ: \(48\) km

Đoạn đường còn lại là: \(x - 48\) (km)

Thời gian dự định đi đoạn đường còn lại là:\(\dfrac{{x - 48}}{{48}}\) (giờ)

Vận tốc lúc sau là: \( 48 + 6 = 54 (km/h) \)

Thời gian thực tế đi đoạn đường còn lại là:\(\dfrac{{x - 48}}{{54}}\) (giờ)

Do bị tàu hỏa chắn đường trong \(10\) phút \(=\dfrac{1}{6}\) giờ nên thời gian thực tế ô tô đi đoạn đường còn lại ít hơn dự định là \(\dfrac{1}{6}\) giờ do đó ta có phương trình: 

\(\dfrac{{x - 48}}{{48}} - \dfrac{{x - 48}}{{54}} = \dfrac{1}{6}\)

\( \Leftrightarrow \dfrac{{9\left( {x - 48} \right)}}{{432}} - \dfrac{{8\left( {x - 48} \right)}}{{432}} = \dfrac{{72}}{{432}}\)

\(⇔9\left( {x - 48} \right) - 8\left( {x - 48} \right) = 72\) 

\(⇔9x - 432 - 8x + 384 = 72\)

\( \Leftrightarrow x - 48 = 72\)

\( \Leftrightarrow x = 72 + 48\)

\(⇔x = 120\) (thỏa điều kiện đặt ra).

Vậy quãng đường AB dài \(120\) km.

a) Hãy viết biểu thức biểu thị:

+ Số tiền lãi sau tháng thứ nhất;

+ Số tiền (cả gốc lẫn lãi) có được sau tháng thứ nhất;

+ Tổng số tiền lãi có được sau tháng thứ hai.

b) Nếu lãi suất là \(1,2\%\) (tức là \(a = 1,2\)) và sau 2 tháng tổng số tiền lãi là 48,288 nghìn đồng, thì lúc đầu bà An đã gửi bao nhiêu tiền tiết kiệm?

Phương pháp giải

a) Áp dụng công thức:

Tiền lãi = Tiền vốn \(\times\) lãi suất. 

Sau tháng thứ nhất thì tiền vốn tháng thứ hai được tính theo công thức là:

Tiền vốn tháng thứ hai = Tiền vốn ban đầu + Tiền lãi tháng thứ nhất.

b) Thay \(a=1,2\) vào biểu thức tìm được ở câu a) rồi tìm x.

Hướng dẫn giải

Câu a

Bà An gửi vào quỹ tiết kiệm: \(x\) nghìn đồng

Lãi suất là \(a\%\) một tháng nên số tiền lãi sau tháng thứ nhất \(a\% .x\) (nghìn đồng)

Số tiền (cả gốc lẫn lãi) có được sau tháng thứ nhất: \(x + a\% .x = \left( {1 + a\% } \right)x\) (nghìn đồng)

Do đó vốn gửi tháng thứ hai là \(\left( {1 + a\% } \right)x\) (nghìn đồng)

Số tiền lãi của tháng thứ hai là: \(\left( {1 + a\% } \right)x.a\% \) (nghìn đồng)

Tổng số tiền lãi sau hai tháng là:

 \(a\% x + \left( {1 + a\% } \right)x.a\% \)\( = \left( {2 + a\% } \right).a\% x\) (nghìn đồng)

Câu b

Vì sau hai tháng bà An lãi \(48288\) đồng với lãi suất \(1,2\%\) nên thay \(a=1,2\) vào biểu thức \( \left( {2 + a\% } \right).a\% x\) ta được: 

\(\eqalign{
& \left( {2 + 1,2\% } \right).1,2\% x = 48288 \cr 
& \Leftrightarrow \left( {2 + {{1,2} \over {100}}} \right).{{1,2} \over {100}}x = 48288 \cr 
& \Leftrightarrow \left( {2 + 0,012} \right).0,012x = 48288 \cr 
& \Leftrightarrow 2,012.0,012x = 48288 \cr 
& \Leftrightarrow x = {{48288} \over {2,012.0,012}} \cr 
& \Leftrightarrow x = 2000000 \cr} \)

Vậy bà An đã gửi tiết kiệm \(2000 000\) đồng.

Năm ngoái, tổng số dân của hai tỉnh A và B là \(4\) triệu. Năm nay, dân số của tỉnh A tăng thêm \(1,1\%\), còn dân số của tỉnh B tăng thêm \(1,2\%\). Tuy vậy, số dân của tỉnh A năm nay vẫn nhiều hơn tỉnh B là \(807200\) người. Tính số dân năm ngoái của mỗi tỉnh.

Phương pháp giải

Bước 1: Đặt số dân năm ngoái của tỉnh A là ẩn, đặt điều kiện cho ẩn.

Bước 2: Biểu diễn các đại lượng còn lại theo ẩn.

Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó.

Bước 4: Kết luận.

Hướng dẫn giải

Gọi \(x\) là số dân năm ngoái của tỉnh A (người) \((0 < x < 4 000 000; x ∈\mathbb N)\)

Số dân năm ngoái của tỉnh B: \(4000 000 - x\) người 

Do dân số của tỉnh A tăng thêm \(1,1\%\) nên số dân của tỉnh A năm nay là: \(x+1,1\%x=1,011.x\) người 

Do dân số của tỉnh B tăng thêm \(1,2\%\) nên số dân của tỉnh B năm nay là:

\(4000000 - x+1,2\%(4000000 - x)\)\(=1,012 (4000000 - x )\) người  

Vì dân số tỉnh A năm nay hơn tỉnh B là \(807200\) người nên ta có phương trình:

 \(1,011x - 1,012\left( {4000000 - x} \right) \)\(= 807200\)

⇔\(1,011x - 4048000 + 1,012x = 807200\)

⇔\(2,023x = 4855200\)

⇔ \(x = 2 400 000\) (thỏa điều kiện đặt ra)

Vậy dân số của tỉnh A là: \(2 400 000\) người

Dân số của tỉnh B là: \(4000 000-2400 000=1 600 000\) người

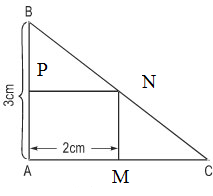
Đố: Lan có một miếng bìa hình tam giác ABC vuông tại A, cạnh AB = 3cm. Lan tính rằng nếu cắt từ miếng bìa đó ra một hình chữ nhật ấy có diện tích bằng một nửa diện tích của miếng bìa ban đầu. Tính độ dài cạnh AC của tam giác ABC.

Phương pháp giải

Bước 1: Đặt độ dài cạnh AC là ẩn, đặt điều kiện cho ẩn

Bước 2: Biểu diễn các đại lượng còn lại theo ẩn.

Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó.

Bước 4: Kết luận.

Hướng dẫn giải

Gọi \(x (cm)\) là độ dài cạnh \(AC (x >2 )\).

Gọi hình chữ nhật là \(MNPA\) (như hình vẽ) thì \(MC = x – 2 (cm)\)

Vì \(MN // AB\) nên \(\dfrac{{MN}}{{AB}} = \dfrac{{MC}}{{AC}}\) (hệ quả của định lí TaLet)

\( \Rightarrow MN = \dfrac{{AB.MC}}{{AC}} = \dfrac{{3\left( {x - 2} \right)}}{x}(cm)\)

Diện tích hình chữ nhật \(MNPA\) là: \(2.\dfrac{{3\left( {x - 2} \right)}}{x} = \dfrac{{6\left( {x - 2} \right)}}{x}\) 

Diện tích hình tam giác \(ABC\) là: \(\dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.x = \dfrac{3}{2}x\)

Vì diện tích hình chữ nhật \(MNPA\) bằng một nửa diện tích hình tam giác \(ABC\) nên ta có phương trình:

\(\eqalign{
& {3 \over 2}x = 2.{{6\left( {x - 2} \right)} \over x} \cr
& \Leftrightarrow {{3x.x} \over {2x}} = {{2.2.6\left( {x - 2} \right)} \over {2x}} \cr
& \Rightarrow 3{x^2} = 24x - 48 \cr
& \Leftrightarrow 3{x^2} - 24x + 48 = 0 \cr
& \Leftrightarrow {x^2} - 8x + 16 = 0 \cr
& \Leftrightarrow {x^2} - 2.x.4 + {4^2} = 0 \cr
& \Leftrightarrow {\left( {x - 4} \right)^2} = 0 \cr
& \Leftrightarrow x - 4 = 0 \cr
& \Leftrightarrow x = 4\text{ (thỏa mãn)} \cr} \)

Vậy \(AC = 4cm\).