Giải bài tập SGK Toán 8 Bài 2: Diện tích hình chữ nhật

Diện tích hình chữ nhật thay đổi như thế nào nếu:

a) Chiều dài tăng \(2\) lần, chiều rộng không đổi?

b) Chiều dài và chiều rộng tăng \(3\) lần?

c) Chiều dài tăng \(4\) lần, chiều rộng giảm \(4\) lần?

Phương pháp giải

Áp dụng: Công thức tính diện tích hình chữ nhật là \(S = a.b\).

Hướng dẫn giải

Giả sử hình chữ nhật ban đầu có chiều dài là \(a\), chiều rộng là \(b\)

Diện tích ban đầu của hình chữ nhật là: \(S = a.b\).

Câu a: Nếu chiều dài tăng \(2\) lần, chiều rộng không đổi thì kích thước chiều dài và chiều rộng của hình chữ nhật mới là \(a' = 2a, b' = b\).

Diện tích hình chữ nhật mới là: \(S'=a'.b' = 2a.b \)\(= 2ab = 2S\).

Vậy diện tích hình chữ nhật mới  gấp \(2\) lần diện tích hình chữ nhật ban đầu.

Câu b: Nếu chiều dài và chiều rộng tăng \(3\) lần thì kích thước chiều dài và chiều rộng của hình chữ nhật mới là \(a' = 3a, b'= 3b\).

Diện tích hình chữ nhật mới là: \(S' =a'.b'= 3a.3b \)\(= 9ab = 9S\).

Vậy diện tích hình chữ nhật mới gấp \(9\) lần diện tích hình chữ nhật ban đầu.

Câu c: Nếu chiều dài tăng \(4\) lần, chiều rộng giảm \(4\) lần thì kích thước chiều dài và chiều rộng của hình chữ nhật mới là \(a' = 4a,\) \(b'= \dfrac{b}{4}\).

Diện tích hình chữ nhật mới là \(S' =a'.b'\)\(= 4a.\dfrac{b}{4}= ab = S.\) 

Vậy diện tích hình chữ nhật không đổi. 

Một gian phòng có nền hình chữ nhật với kích thước là \(4,2\,m\) và \(5,4\,m\) có một cửa sổ hình chữ nhật kích thước là \(1\,m\) và \(1,6\,m\) và một cửa ra vào hình chữ nhật kích thước là \(1,2\,m\) và \(2\,m.\)

Ta coi một gian phòng đạt mức chuẩn về ánh sáng nếu diện tích các cửa bằng \(20\%\) diện tích nền nhà. Hỏi gian phòng trên có đạt mức chuẩn về ánh sáng hay không?

Phương pháp giải

Áp dụng: công thức tính diện tích hình chữ nhật.

\(S = a.b\)

(\(S\) là diện tích, \(a\) là chiều dài, \(b\) là chiều rộng của hình chữ nhật)

Hướng dẫn giải

Diện tích nền nhà là: \(S = 4,2.5,4 = 22,68\) (\({m^2}\))

Diện tích cửa sổ là: \({S_1}= 1. 1,6 = 1,6\) (\({m^2}\))

Diện tích cửa ra vào là: \({S_2}=1,2.2 = 2,4\) (\({m^2}\))

Diện tích các cửa là: \(S' = {S_1} + {S_2}= 1,6 + 2,4 = 4\) (\({m^2}\))

Ta có \(\dfrac{S^{'}}{S} = \dfrac{4}{22,68}.100\%≈ 17,64\% < 20\%.\) 

Vậy gian phòng không đạt mức chuẩn về ánh sáng

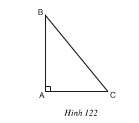
Đo cạnh (đơn vị mm) rồi tính diện tích tam giác vuông dưới đây (h.122):

Phương pháp giải

- Dùng thước đo hai cạnh của góc vuông.

- Áp dụng: công thức tính diện tích tam giác vuông: Diện tích tam giác vuông bằng nửa tích của hai cạnh góc vuông.  

Hướng dẫn giải

Đo hai cạnh góc vuông, ta được \(AB= 30\,mm, AC= 25\,mm\).

Áp dụng công thức tính diện tích tam giác vuông, ta có diện tích tam giác \(ABC\) là: 

\(S = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.30.25 = 375\,m{m^2}\)

Vậy \(S = 375m{m^2}\)

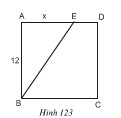
\(ABCD\) là một hình vuông cạnh \( 12cm\), \(AE = x(cm)\) (h.\(123\)). Tính \(x\) sao cho diện tích tam giác \(ABE\) bằng \(\dfrac{1}{3}\) diện tích hình vuông \(ABCD\).

Phương pháp giải

Áp dụng:

+) Công thức tính diện tích tam giác vuông: Diện tích tam giác vuông bằng nửa tích của hai cạnh góc vuông.

+) Công thức tính diện tích hình vuông: Diện tích hình vuông bằng bình phương cạnh của nó.

Hướng dẫn giải

Diện tích tam giác vuông \(ABE\) là: \(S' = \dfrac{1}{2}AB.A{\rm{E}} = \dfrac{1}{2}.12.x = 6x\left( {c{m^2}} \right)\)

Diện tích hình vuông là: \(S = 12.12 = 144\left( {c{m^2}} \right)\)

Theo đề bài ta có: \(S' = \dfrac{S}{3}\)

\(\Rightarrow 6x = \dfrac{{144}}{3} \)

\(\Rightarrow 6x= 48\)

\( \Rightarrow x = 48:6 = 8\left( {cm} \right)\).

Vậy \(x = 8cm\).

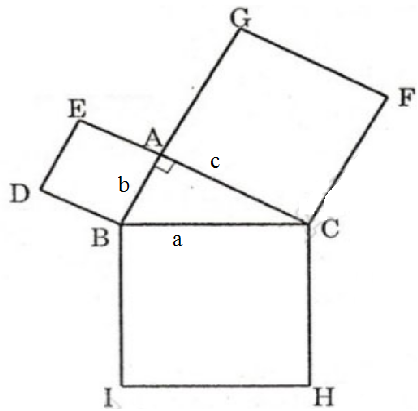
Cho một tam giác vuông. Hãy so sánh tổng diện tích của hai hình vuông dựng trên hai góc vuông với diện tích hình vuông dựng trên cạnh huyền.

Phương pháp giải

- Áp dụng công thức tính diện tích hình vuông: Diện tích hình vuông bằng bình phương độ dài 1 cạnh.

- Định lí Pytago: Bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

Hướng dẫn giải

Giả sử tam giác vuông \(ABC\) có cạnh huyền là \(a\) và hai cạnh góc vuông là \(b, c\) (như hình vẽ)

Diện tích hình vuông dựng trên cạnh huyền \(a\) là \({a^2}\)

Diện tích hình vuông dựng trên cạnh góc vuông \(b\) là \({b^2}\)

Diện tích hình vuông dựng trên cạnh góc vuông \(c\) là \( {c^2}\)

Áp dụng định lí Pitago vào tam giác vuông \(ABC\) vuông tại \(A\) ta có:  \({a^2} = {b^2} + {c^2}\)

Vậy: Trong một tam giác vuông, tổng diện tích của hai hình vuông dựng trên hai cạnh góc vuông bằng diện tích hình vuông dựng trên cạnh huyền.

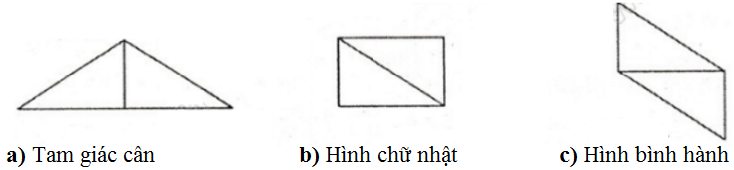
Cắt hai tam giác vuông bằng nhau từ một tấm bìa. Hãy ghép hai tam giác đó để tạo thành:

a) Một tam giác cân

b) Một hình chữ nhật

c) Một hình bình hành.

Diện tích các hình này có bằng nhau không? Vì sao?

Phương pháp giải

Áp dụng tính chất diện tích đa giác: 

- Hai tam giác bằng nhau thì có diện tích bằng nhau.

- Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của nó bằng tổng diện tích của những đa giác đó.

Hướng dẫn giải

Ta ghép như sau

Diện tích 3 hình này đều bằng nhau vì cùng bằng tổng diện tích của hai tam giác vuông ban đầu.

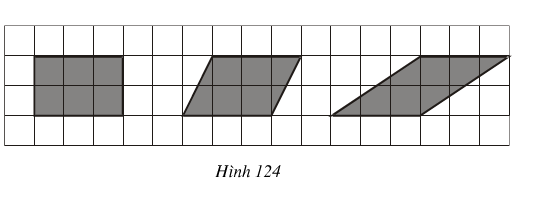
Tính diện tích các hình dưới đây (h.\(124\)) (mỗi ô vuông là \(1\) đơn vị diện tích)

Phương pháp giải

Áp dụng công thức tính diện tích: 

+ Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông.

+ Diện tích hình chữ nhật bằng tích của chiều dài và chiều rộng

+ Diện tích hình vuông cạnh \(a\) bằng \(a^2\)

Hướng dẫn giải

Theo đề bài: mỗi ô vuông là \(1\) đơn vị diện tích nên mỗi cạnh của hình vuông sẽ có độ dài là \(1\) đơn vị.

- Hình thứ nhất là một hình chữ nhật có diện tích là: \(2.3 = 6\) (đơn vị diện tích)

- Hình thứ hai ta vẽ thêm 2 nét đứt như trên hình vẽ, khi đó:

Diện tích hình thứ hai \(=\) diện tích hình vuông \(+\) \(2 \times \) diện tích tam giác.

\(S_2 = 2.2 + 2.\dfrac{1}{2}.1.2 = 6\) (đơn vị diện tích)

- Hình thứ ba: ta vẽ thêm \(1\) nét đứt như trên hình, khi đó:

Diện tích hình thứ ba \(= 2 \times \) diện tích tam giác

\(S_3=2.\dfrac{1}{2}.3.2 = 6\) (đơn vị diện tích)

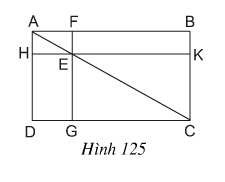
Cho hình \(125\), trong đó \(ABCD\) là hình chữ nhật, \(E\) là một điểm bất kì nằm trên đường chéo \(AC, FG // AD\), và \(HK // AB\).

Chứng minh rằng hai hình chữ nhật \(EFBK\) và \(EGDH\) có cùng diện tích. 

Phương pháp giải

Áp dụng tính chất: Hai tam giác bằng nhau thì có diện tích bằng nhau.

Hướng dẫn giải

\(ABCD\) là hình chữ nhật nên \(AB//CD;\;AD//BC\)

Vì \(FG// AD\) (gt) nên suy ra \(EG//KC\)

Vì \(HK//DC\) (vì cùng song song với \(AB\)) nên suy ra \(EK//GC\) 

\( \Rightarrow \) Tứ giác \(EKCG\) là hình bình hành (dấu hiệu nhận biết hình bình hành)

Mặt khác, \(\widehat {GCK} = {90^0}\) (gt) do đó \(EKCG\) là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

Xét \(\Delta ECG\) và \(\Delta CEK\) có:

+) \(EG=KC\) (vì \(EKCG\) là hình chữ nhật)

+) \(EC\) chung (gt)

+) \(EK=CG\) (vì \(EKCG\) là hình chữ nhật)

\(\Rightarrow \Delta ECG = \Delta CEK\) (c-c-c)

Do đó: \({S_{ECG}} = {S_{CEK}}\)    (1)   (Hai tam giác bằng nhau thì có diện tích bằng nhau)

Tương tự:

Vì \(ABCD\) là hình chữ nhật nên \(AB=DC, AD=BC, \widehat D=\widehat B=90^0\)

\(\Rightarrow \Delta ADC = \Delta CBA\) (c-g-c)

Do đó: \({S_{ ADC}} = {S_{CBA}}\)      (2)

Vì \(AF//HE, AH//EF\) nên \(AHEF\) là hình bình hành. Lại có \(\widehat A=90^0\) (do ABCD là hình chữ nhật) nên \(AHEF\) là hình chữ nhật. 

Suy ra \(AF=HE, AH=FE, \widehat H=\widehat F=90^0\) (tính chất)

\(\Rightarrow \Delta AHE = \Delta EFA\) (c-g-c)

Do đó: \({S_{AHE}} = {S_{ EFA}}\)       (3)

Ta có: 

\(\eqalign{
& {S_{ADC}} = {S_{AHE}} + {S_{EGDH}} + {S_{ECG}} \cr
& {S_{CBA}} = {S_{EFA}} + {S_{EFBK}} + {S_{CEK}} \cr} \)

Kết hợp với (2) \(\Rightarrow {S_{AHE}} + {S_{EGDH}} + {S_{ECG}} = {S_{EFA}} \)\(+ {S_{EFBK}} + {S_{CEK}}\) 

Kết hợp với (1) và (3) \(\Rightarrow {S_{EGDH}} = {S_{EFBK}}\)

Một đám đất hình chữ nhật dài \(700m\), rộng \(400m\). Hãy tính diện tích đám đất đó theo đơn vị \({m^2},k{m^2},a,ha\).

Phương pháp giải

Áp dụng công thức tính diện tích hình chữ nhật, qui tắc đổi đơn vị diện tích.

\(1k{m^2} = 1000000\,({m^2})\), \(1\,a=100m^2,1\,ha=10000m^2\)

Hướng dẫn giải

Diện tích đám đất hình chữ nhật đó theo đơn vị \({m^2}\) là:

\(S = 700.400 = 280000{\rm{ }}({m^2})\)

Ta có: \(1k{m^2} = 1000000\,({m^2})\)       

\(\begin{array}{*{20}{l}}
{1a = 100\,({m^2})}\\
{1ha = 10000\left( {{m^2}} \right)}
\end{array}\)

Nên diện tích đám đất tính theo các đơn vị trên là:

\(S = 0,28k{m^2} = 2800a = 28ha.\)

Đố. Vẽ hình chữ nhật \(ABCD\) có \(AB = 5\,cm, BC = 3\,cm.\)

a) Hãy vẽ một hình chữ nhật có diện tích nhỏ hơn nhưng có chu vi lớn hơn hình chữ nhật \(ABCD.\) Vẽ được mấy hình như vậy.

b) Hãy vẽ hình vuông có chu vi bằng chu vi hình chữ nhật \(ABCD.\) Vẽ được mấy hình vuông như vậy? So sánh diện tích hình chữ nhật với diện tích hình vuông có cùng chu vi vừa vẽ. Tại sao trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.

Phương pháp giải

Áp dụng công thức tính diện tích hình chữ nhật, diện tích hình vuông.

Hướng dẫn giải

Câu a

Hình chữ nhật \(ABCD\) đã cho có diện tích là \({S_{ABCD}} = 3.5 = 15\,(c{m^2}).\)

Chu vi hình chữ nhật \(ABCD\) là \((5+3).2=16\;(cm)\)

- Hình chữ nhật có chiều rộng là \(1\,cm\), chiều dài là \(12\,cm\) có diện tích là \(12c{m^2}<{S_{ABCD}}\) và chu vi là \(( 1+12).2 = 26\,(cm)\) (có \(26>16\)).

- Hình chữ nhật có chiều rộng là \(2\,cm\), chiều dài là \(7\,cm\) có diện tích là \(14c{m^2}<{S_{ABCD}}\) và chu vi là \((2+7).2 = 18\,(cm)\) (có \(18 > 16\)).

Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật \(ABCD\) cho trước.

Câu b

Chu vi hình chữ nhật \(ABCD\) đã cho là: \((5+3).2 = 16 \,(cm)\)

Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật \(ABCD\) là: \(16 : 4 = 4\,(cm).\)

Diện tích hình vuông này là \(4.4 = 16 ({cm^2})\) 

Vậy \({S_{hcn}} < {S_{hv}}\)

Vẽ được một hình vuông như vậy.

+) Tổng quát:  Giả sử hình chữ nhật có các kích thước là \(a, b\). Khi đó: 

- Diện tích của hình chữ nhật đó là: \(ab\)

- Chu vi hình chữ nhật đó là: \(2.(a+b)\) 

- Cạnh của hình vuông có chu vi bằng chu vi hình chữ nhật là: \(\dfrac{{2.(a + b)}}{4}=\dfrac{{a + b}}{2}\)

Vậy diện tích hình vuông đó là: \({\left( {\dfrac{{a + b}}{2}} \right)^2}\)

Ta có:

\({\left( {\dfrac{{a + b}}{2}} \right)^2} = \dfrac{{{{\left( {a + b} \right)}^2}}}{4} \)\(\,= \dfrac{{{a^2} + 2{\rm{a}}b + {b^2}}}{4}\)\( = \dfrac{{{{\left( {a - b} \right)}^2} + 4{\rm{a}}b}}{4} \)\(\,= \dfrac{{{{\left( {a - b} \right)}^2}}}{4} + ab \ge ab\)

( vì \(\dfrac{{{{\left( {a - b} \right)}^2}}}{4} \ge 0\) với mọi \(\,a,\,b\))

Vậy trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.