Giải bài tập SGK Toán 8 Bài: Luyện tập
Nội dung giải bài tập trang 104, 105 SGK Toán 8 bài Luyện tập bên dưới đây sẽ giúp các em học thật tốt môn Toán. Qua tài liệu này các em sẽ nắm được phương pháp giải cụ thể của từng bài từ đó đưa ra lời giải phù hợp với đề ra. Mời các em cùng tham khảo.
Mục lục nội dung

1. Giải bài 14 trang 104 SGK Toán 8 tập 2
Một bể nước hình hộp chữ nhật có chiều dài \(2m\). Lúc đầu bể không có nước. Sau khi đổ vào bể \(120\) thùng nước, mỗi thùng chứa \(20\) lít thì mực nước của bể cao \(0,8m\).
a) Tính chiều rộng của bể nước.
b) Người ta đổ thêm vào bể \(60\) thùng nước nữa thì đầy bể. Hỏi bể cao bao nhiêu mét?
Phương pháp giải
Giả sử \( a\) là chiều dài, \( b\) là chiều rộng và \( c\) là chiều cao.
Ta áp dụng các công thức sau:
\(V = a.b.c\)
\(b= V :( a.c)\)
\(c= V :S_{\mbox{1 đáy}} = V : (a.b)\)
Hướng dẫn giải
a) Thể tích nước đổ vào là:
\(120 . 20 = 2400 (l) =2400dm^3= 2,4\) \((m^3) \)
Chiều rộng của bể nước là:
\(2,4 : (2 . 0,8) = 1,5 (m)\)
b) Thể tích nước đổ thêm vào bể là :
\(60 . 20 = 1200 (l) =1200dm^3= 1,2\) \((m^3) \)
Thể tích của bể nước là:
\(2,4 +1,2 = 3,6(m^3) \)
Chiều cao của bể nước là:
\(3,6 : (2 . 1,5) = 1,2(m) \).
2. Giải bài 15 trang 105 SGK Toán 8 tập 2
Một cái thùng hình lập phương, cạnh \(7dm\), có chứa nước với độ sâu của nước là \(4dm\). Người ta thả \(25\) viên gạch có chiều dài \(2dm\), chiều rộng \(1dm\) và chiều cao \(0,5dm\) vào thùng. Hỏi nước trong thùng dâng lên cách miệng thùng bao nhiêu đề-xi-mét? (Giả thiết toàn bộ gạch ngập trong nước và chúng hút nước không đáng kể).
Phương pháp giải
- Tính thể tích nước đã có trong thùng, tức là tính thể tích của hình hộp chữ nhật có chiều dài \(7dm\), chiều rộng \(7dm\) và chiều cao \(4dm\)
- Tính thể tích của \(25 \) viên gạch, tức là tìm \(25 \) lần thể tích hình hộp chữ nhật có chiều dài \(2dm\), chiều rộng \(1dm\) và chiều cao \(0,5dm\)
- Tính thể tích của nước và gạch.
- Tính chiều cao mực nước trong thùng sau khi thả \(25\) viên gạch = thể tích của nước và gạch: diện tích đáy.
- Khoảng cách giữa nước và miệng thùng = chiều cao của thùng - chiều cao mực nước trong thùng sau khi thả \(25\) viên gạch.
Hướng dẫn giải
Thể tích của nước trong thùng là:
\( 7 . 7 . 4 = 196 (dm^3) \)
Thể tích của \(25\) viên gạch:
\(25 . (2 . 1 . 0,5) = 25 (dm^3) \)
Thể tích của nước và gạch:
\( 196 + 25 = 221(dm^3) \)
Chiều cao mực nước trong thùng sau khi thả \(25\) viên gạch vào là:
\( 221 : (7.7) ≈ 4,51 (dm) \)
Nước trong thùng dâng lên cách miệng thùng số đề-xi-mét là :
\(7 - 4,51 = 2,49 (dm) \)
3. Giải bài 16 trang 105 SGK Toán 8 tập 2
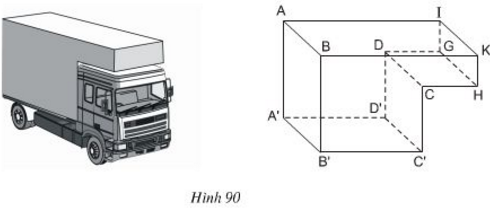
Thùng chứa của một xe chở hàng đông lạnh có dạng như hình 90. Một số mặt là những hình chữ nhật, chẳng hạn (ABKI), (DCC'D'), ... . Quan sát hình và trả lời các câu hỏi sau:
a) Những đường thẳng nào song song với mặt phẳng (ABKI)?
b) Những đường thẳng nào vuông góc với mặt phẳng (DCC'D')?
c) Mặt phẳng (A'D'C'B') có vuông góc với mặt phẳng (DCC'D') hay không?
Phương pháp giải
a) Áp dụng lý thuyết về đường thẳng song song với mặt phẳng
+ Một đường thẳng d song song với một mặt phẳng P nếu đường thẳng d song song với một đường thẳng a nằm trong P.
b) Áp dụng lý thuyết về đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với một mặt phẳng nếu đường thẳng đó vuông góc với hai đường thẳng cắt nhau trong mặt phẳng.
c) Áp dụng lý thuyết về hai mặt phẳng vuông góc.
Hướng dẫn giải
a) Những đường thẳng song song với mặt phẳng \((ABKI)\) là : \(A’B’; D’C’; DC; GH.\)
b) Những đường thẳng vuông góc với mặt phẳng \((DCC’D’)\) là : \(A’D’; B’C’; DG; CH; AI; BK.\)
c) Ta có \(A’D’\) vuông góc với mặt phẳng \((DCC'D')\) nên suy ra hai mặt phẳng \((A’B’C’D’)\) và \( (DCC'D’)\) vuông góc với nhau.
4. Giải bài 17 trang 105 SGK Toán 8 tập 2
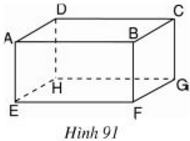
Cho hình hộp chữ nhật ABCD.EFGH (h.91).
a) Kể tên các đường thẳng song song với mp (EFGH).
b) Đường thẳng AB song song với những mặt phẳng nào?
c) Đường thẳng AD song song với những đường thẳng nào?
Phương pháp giải
- Hai đường thẳng \(a\) và \(b\) gọi là song song với nhau nếu chúng nằm trong cùng một mặt phẳng và không có điểm chung.
- Khi đường thẳng \(d\) không nằm trong mặt phẳng \((ABCD)\) mà \(d\) song song với đường thẳng của mặt phẳng này thì ta nói đường thẳng \(d\) song song với mặt phẳng \((ABCD)\).
Hướng dẫn giải
a) Những đường thẳng song song với mp\( (EFGH)\) là: \(AB; BC; CD; DA.\)
(Vì AB//EF, BC//FG, DC//HG, AD//EH)
b) Đường thẳng \(AB\) song song với các mặt phẳng: \((CDHG); (EFGH); (DCFE).\)
c) Trong \(mp(ABCD)\), \(AD//BC\) (1)
Trong \(mp(ADHE)\), \(AD//HE\) (2)
Trong \(mp(BCGF)\), \(GF//BC\) (3)
Từ (1),(3): \(AD//BC\) và \(GF//BC\), do đó \(AD//GF\).
Vậy đường thẳng \(AD\) song song với các đường thẳng: \(BC; FG; EH.\)
5. Giải bài 18 trang 105 SGK Toán 8 tập 2
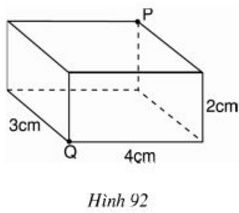
Đố: Các kích thước của môt hình hộp chữ nhật là 4cm, 3cm và 2cm. Một con kiến bò theo mặt của hình hộp đó từ Q dến P (h.92).
a) Hỏi con kiến bò theo đường nào là ngắn nhất?
b) Độ dài ngắn nhất đó là bao nhiêu xentimet?
Phương pháp giải
Áp dụng: Định lí Pytago, so sánh hai số vô tỉ.
Hướng dẫn giải
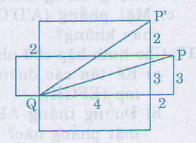
a) Vì con kiến bò theo mặt của hình hộp từ \(Q\) đến \(P\) tức phải bò trên “ một mặt phẳng” ta vẽ hình khai triển của hình hộp chữ nhật và trải phẳng như sau:
Khi đó, \(P\) sẽ có hai vị trí là \(P’\) và \(P’’\) và quãng đường ngắn nhất sẽ là một trong hai đoạn thẳng \(QP’ \) và \(QP’’\) Ta có:
Hình chữ nhật với chiều dài \(2+3=5cm\) và chiều rộng \( 4cm\) có đường chéo \(QP’\) với độ dài:
\(QP’ = \sqrt{4^{2}+ 5^{2}} =\sqrt{41}cm \)
Hình chữ nhật với chiều dài \(4+2=6cm\) và chiều rộng \( 3cm\) có đường chéo \(QP’'\) với độ dài:
\(QP’’ = \sqrt{6^{2}+ 3^{2}}=\sqrt{45}cm \)
Ta có: \( \sqrt{41} < \sqrt{45} \) . Vậy đường đi ngắn nhất là \(QP’\)
b) Vậy độ dài ngắn nhất là \( \sqrt{41} \approx 6,4 cm\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 8 Bài 1: Hình hộp chữ nhật
- doc Giải bài tập SGK Toán 8 Bài 2: Hình hộp chữ nhật (tiếp theo)
- doc Giải bài tập SGK Toán 8 Bài 3: Thể tích của hình hộp chữ nhật
- doc Giải bài tập SGK Toán 8 Bài 4: Hình lăng trụ đứng
- doc Giải bài tập SGK Toán 8 Bài 5: Diện tích xung quanh của hình lăng trụ đứng
- doc Giải bài tập SGK Toán 8 Bài 6: Thể tích của hình lăng trụ đứng
- doc Giải bài tập SGK Toán 8 Bài: Luyện tập
- doc Giải bài tập SGK Toán 8 Bài 7: Hình chóp đều và hình chóp cụt đều
- doc Giải bài tập SGK Toán 8 Bài 8: Diện tích xung quanh của hình chóp đều
- doc Giải bài tập SGK Toán 8 Bài 9: Thể tích của hình chóp đều
- doc Giải bài tập SGK Toán 8 Bài: Luyện tập