Giải bài tập SGK Toán 8 Bài 1: Định lí Ta-lét trong tam giác

Viết tỉ số của hai đoạn thẳng có độ dài như sau:

a) $AB = 5cm$ và $CD = 15 cm$

b) $EF = 48cm$ và $GH = 16dm$

c) $PQ = 1,2m$ và $MN = 24cm$

Phương pháp giải

Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

Ví dụ : $AB = 5cm$ và $CD = 15 cm$

$\Rightarrow \dfrac{AB}{CD} = \dfrac{5}{15} = \dfrac{1}{3}$

Hướng dẫn giải

a) $AB = 5cm$ và $CD = 15 cm$

$\Rightarrow \dfrac{AB}{CD} = \dfrac{5}{15} = \dfrac{1}{3}$

b) $EF = 48cm = 4,8 dm$ và $GH = 16dm$

$\Rightarrow \dfrac{EF}{GH} = \dfrac{4,8}{16} = \dfrac{3}{10}$

c) $PQ = 1,2m = 120cm$ và $MN = 24cm$

$\Rightarrow \dfrac{PQ}{MN} = \dfrac{120}{24} = 5$

Cho biết  $\dfrac{AB}{CD} = \dfrac{3}{4}$ và $CD= 12cm$. Tính độ dài $AB$.

Phương pháp giải

Áp dụng tính chất của hai tỉ số bằng nhau.

$\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow ad = bc$

Hướng dẫn giải

Ta có: $\dfrac{AB}{CD} = \dfrac{3}{4}$  mà $CD= 12cm$ nên

$\dfrac{AB}{12}=\dfrac{3}{4}$ 

$\Rightarrow  AB= \dfrac{12.3}{4} = 9cm$.

Vậy $AB= 9cm$.

Cho biết độ dài cùa $AB$ gấp $5$ lần độ dài của $CD$ và độ dài của $A'B'$ gấp $12$ lần độ dài của $CD$. Tính tỉ số của hai đoạn thẳng $AB$ và \(A'B'\

Phương pháp giải

Biểu diễn độ dài của đoạn thẳng $AB$ và $A'B'$ theo $CD$. Sau đó lập tỉ số.

Hướng dẫn giải

Độ dài $AB$ gấp $5$ lần độ dài $CD$ nên $AB= 5CD$.

Độ dài $A'B'$ gấp $12$ lần độ dài $CD$ nên $A'B'= 12CD$.

$\Rightarrow$ Tỉ số của hai đoạn thẳng $AB$ và $A'B'$ là: 

$\dfrac{AB}{A'B'}= \dfrac{5CD}{12CD} = \dfrac{5}{12}$

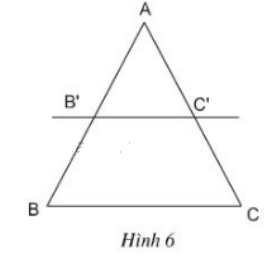
Cho biết $\dfrac{AB'}{AB} = \dfrac{AC'}{AC}$ (h.6). Chứng minh rằng:

a) $\dfrac{AB'}{B'B} = \dfrac{AC'}{C'C};$

b) $\dfrac{BB'}{AB} = \dfrac{CC'}{AC}.$

Phương pháp giải

a) $\dfrac{AB'}{AB}=\dfrac{AC'}{AC}$ (giả thiết) $\Rightarrow \dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AB}}{{AB'}} - 1$

$\dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AC - AC'}}{{AC'}} = \dfrac{{C'C}}{{AC'}}$

$\dfrac{{AB}}{{AB'}} - 1 = \dfrac{{AB - AB'}}{{AB'}} = \dfrac{{B'B}}{{AB'}}$

Từ đó suy ra được điều cần chứng minh

b) Chứng minh $\dfrac{AB-BB'}{AB} = \dfrac{AC -CC'}{AC}$ $\Rightarrow 1 - \dfrac{{BB'}}{{AB}} = 1 - \dfrac{{CC'}}{{AC}}$

Suy ra điều cần chứng minh

Hướng dẫn giải

a) Ta có: 

$\dfrac{AB'}{AB}=\dfrac{AC'}{AC}$ (giả thiết)

$\Rightarrow \dfrac{AC}{AC'}=\dfrac{AB}{AB'}$

$\Rightarrow \dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AB}}{{AB'}} - 1$

Ta có:

$\dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AC - AC'}}{{AC'}} = \dfrac{{C'C}}{{AC'}}$

$\dfrac{{AB}}{{AB'}} - 1 = \dfrac{{AB - AB'}}{{AB'}} = \dfrac{{B'B}}{{AB'}}$

$\Rightarrow \dfrac{{C'C}}{{AC'}} = \dfrac{{B'B}}{{AB'}} \Rightarrow \dfrac{{AB'}}{{B'B}} = \dfrac{{AC'}}{{C'C}}$ (điều phải chứng minh).

b) Vì $\dfrac{AB'}{AB} = \dfrac{AC'}{AC}$

Mà $AB' = AB - B'B, AC' = AC - C'C$

$\dfrac{AB-BB'}{AB} = \dfrac{AC -CC'}{AC}$ 

$\Rightarrow 1 - \dfrac{{BB'}}{{AB}} = 1 - \dfrac{{CC'}}{{AC}}$

$\Rightarrow \dfrac{BB'}{AB}= \dfrac{CC'}{AC}$ (điều phải chứng minh).

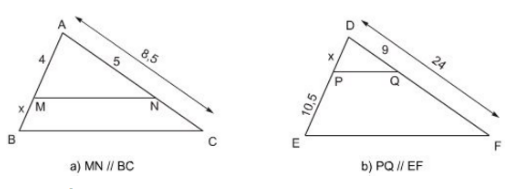
Tính $x$ trong các trường hợp sau

Phương pháp giải

a) Theo định lí Ta-lét ta có:

$\dfrac{BM}{AM} = \dfrac{CN}{AN}$

Mà $CN =AC- AN= 8,5 - 5= 3,5$

Nên $\dfrac{x}{4}= \dfrac{3,5}{5}  \Rightarrow  x$

b) Theo định lí Ta-lét ta có:

$\dfrac{DP}{PE} = \dfrac{DQ}{QF}$

Mà $QF = DF - DQ = 24 - 9 = 15$

Nên $\dfrac{x}{10,5} = \dfrac{9}{15}  \Rightarrow  x$

Hướng dẫn giải

a) $MN // BC$ (giả thiết)

Theo định lí Ta-lét ta có:

$\dfrac{BM}{AM} = \dfrac{CN}{AN}$

Mà $CN =AC- AN= 8,5 - 5= 3,5$

nên $\dfrac{x}{4}= \dfrac{3,5}{5}  \Rightarrow  x = \dfrac{4.3,5}{5} = 2,8$.

Vậy $x = 2,8$.

 b) $PQ // EF$ (giả thiết)

Theo định lí Ta-lét ta có:

$\dfrac{DP}{PE} = \dfrac{DQ}{QF}$

Mà $QF = DF - DQ = 24 - 9 = 15$

Nên $\dfrac{x}{10,5} = \dfrac{9}{15}  \Rightarrow  x = \dfrac{10,5.9}{15} = 6,3$

Vậy $x=6,3$.