Giải bài tập SGK Toán 8 Bài 9: Thể tích của hình chóp đều

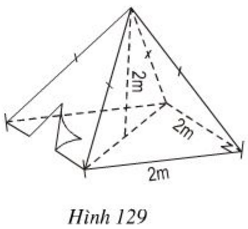
Hình 129 là một cái lều ở trại hè của học sinh kèm theo các kích thước.

a) Thể tích không khí bên trong lều là bao nhiêu?

b) Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp, ... biết √5 ≈ 2,24).

Phương pháp giải

a) Thể tích không khí trong lều bằng thể tích hình chóp có chiều cao \(2cm\), đáy là hình vuông cạnh dài \(2m\). 

Tính thể tích hình chóp theo công thức:   \(V = \dfrac{1}{3} .S.h\), trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.

b) Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh), mỗi mặt là một tam giác cân.

Hướng dẫn giải

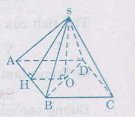
a) Thể tích cần tính bằng thể tích của hình chóp có chiều cao \(2cm\), đáy là hình vuông cạnh dài \(2m\). 

Diện tích đáy là:

\( S_{đ} = 2.2=4(m^2)\)

Thể tích hình chóp là:

\(V = \dfrac{1}{3}.S.h = \dfrac{1}{3}.4.2 = \dfrac{8}{3}\approx 2,67\)\(\,(m^3) \)  

b) Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.

Gọi \(H\) là trung điểm của \(AB\) và \(O\) là tâm của hình vuông \(ABCD\).

Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao \(SH\) của mỗi mặt.

 Theo định lý Pytago trong tam giác vuông SHA, ta có:

 \(SH^2 =SO^2+OH^2 \)\(\,= SO^2+{\left( {\dfrac{{BC}}{2}} \right)^2} \) \(= 2^2+1^2=5\)

\( \Rightarrow SH =\sqrt{5}\approx 2,24(m) \)

Diện tích xung quanh của hình chóp là: 

\( S_{xq} = p.d = \dfrac{1}{2}. 2.4.2,24 = 8,96 (m^2) \)

Tính thể tích của mỗi hình chóp đều dưới đây (h.130, h.131).

Hình 130. Đường cao AO = 12cm, BC = 10cm (\(\sqrt{75} = 8,66\))

Hình 131. Đường cao AO = 16,2cm; BC = 8cm (\(\sqrt{48} = 6,93\))

Phương pháp giải

Tính thể tích hình chóp theo công thức:   \(V = \dfrac{1}{3} .S.h\), trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.

Hướng dẫn giải

Hình 130

Đáy của hình chóp là tam giác đều cạnh bằng \(10cm\) như hình vẽ:

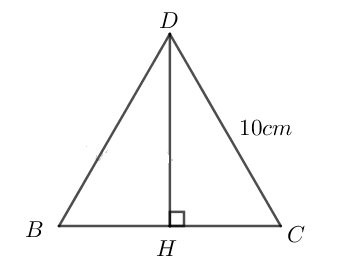
Đường cao của tam giác đều \(BDC\) là:

\(h= HD =\sqrt{DC^{2} - HC^{2}} \) \(= \sqrt{DC^{2} -{\left( {\dfrac{{BC}}{2}} \right)^2}} \)

\(= \sqrt{10^{2} - 5^{2}} = \sqrt{75}\approx 8,66 (cm) \) 

Diện tích đáy của hình chóp đều là:

\(S= \dfrac{1}{2}. BC. h = \dfrac{1}{2}. 10. 8,66 =43,3 \) \((cm^2) \)

Thể tích hình chóp đều là:

\( V= \dfrac{1}{3} .S.AO = \dfrac{1}{3} .43,3 .12 =173,2 \) \((cm^3)\) 

Hình 131

Đáy của hình chóp là tam giác đều cạnh bằng \(8cm\) như hình vẽ:

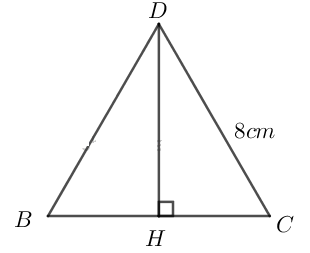
Đường cao của tam giác đều \(BDC\) là:

 \(h= HD =\sqrt{DC^{2} - HC^{2}} \) \(= \sqrt{DC^{2} - {\left( {\dfrac{{BC}}{2}} \right)^2}} \)

 \(= \sqrt{8^{2} - 4^{2}} = \sqrt{48}\approx 6,93 (cm) \) 

Diện tích đáy của hình chóp đều là:

\(S= \dfrac{1}{2}. BC. h = \dfrac{1}{2}. 8. 6,93 =27,72 \) \((cm^2) \)

Thể tích hình chóp đều là:

\( V= \dfrac{1}{3} .S.AO = \dfrac{1}{3} .27,72 .16,2 \)\(\,\approx 149,69\) \( (cm^3)\) 

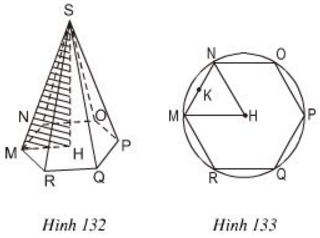
S.MNOPQR là một hình chóp lục giác đều (h.132). Bán kính đường tròn ngoại tiếp đáy (đường tròn tâm H, đi qua sáu đỉnh của đáy) HM = 12cm (h.133), chiều cao SH = 35cm. Hãy tính:

a) Diện tích đáy và thể tích của hình chóp (biết √108 ≈ 10,39)

b) Độ dài cạnh bên SM và diện tích toàn phần của hình chóp (biết √1333 ≈ 36,51).

Phương pháp giải

a) Tính thể tích hình chóp theo công thức:   \(V = \dfrac{1}{3} .S.h\), trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.

b) Sử dụng định lý Pytago 

Diện tích xung quanh bằng nửa chu vi đáy nhân với trung đoạn 

Diện tích toàn phần bằng tổng diện tích xung quanh và diện tích đáy

Hướng dẫn giải

a) Tam giác \(HMN \) là tam giác đều.

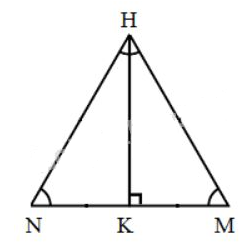
Đường cao của tam giác là:

 \(HK = \sqrt{HM^{2}- KM^{2}}\) \( = \sqrt{HM^{2}- {\left( {\dfrac{{MN}}{2}} \right)^2}} \)

\(= \sqrt{12^{2}- 6^{2}} = \sqrt{108}\approx  10,39(cm) \)

Diện tích đáy của hình chóp lục giác đều chính là \(6\) lần diện tích của tam giác đều \(HMN\).

Diện tích đáy của hình chóp là:  

\(S_{đ} =6.\dfrac{1}{2}. MN. HK = 6.\dfrac{1}{2}. 12. 10,39 \) \(=374,04(cm^2) \) 

Thể tích của hình chóp:

  \(V =\dfrac{1}{3}. S_{đ}. SH = \dfrac{1}{3}. 374,04 . 35 \) \(= 4363,8(cm^3) \) 

b) Trong tam giác vuông \(SMH\) có: 

\(SM= \sqrt{SH^{2}+ MH^{2}} = \sqrt{35^{2}+ 12^{2}}\) \(=\sqrt{1369} = 37 (cm)\) 

Đường cao của mỗi mặt bên là:

 \(d = SK =\sqrt{SM^{2}- KM^{2}} \)

= \(\sqrt{37^{2}- 6^{2}} = \sqrt{1333}\approx 36,51 (cm) \)

Diện tích xung quanh hình chóp là :

\( S_{xq} =  p.d = \dfrac{1}{2}.6. MN. SK \)

\( =\dfrac{1}{2}. 6.12.36,51 = 1314,36 (cm^2)\)

Diện tích toàn phần của hình chóp là:

\(S_{tp} = S_{xq} +S_{đ} = 1314,36 + 374,04 \) \(= 1688,4 (cm^2) \)