Giải bài tập SGK Toán 8 Bài 6: Trường hợp đồng dạng thứ hai

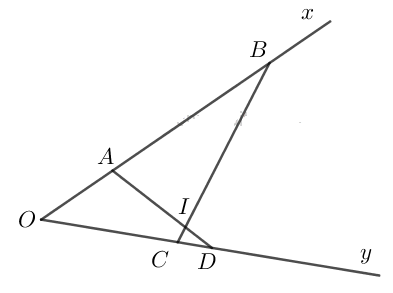
Trên một cạnh của góc $xOy$ ($\widehat {xOy} \ne {180^0}$), Đặt các đoạn thẳng $OA= 5cm, OB= 16cm$. Trên cạnh thứ hai của góc đó, đặt các đoạn $OC= 8cm, OD= 10cm$.

a) Chứng minh hai tam giác $OCB$ và $OAD$ đồng dạng.

b) Gọi giao điểm của các cạnh $AD$ và $BC$ là $I$, chứng minh rằng hai tam giác $IAB$ và $ICD$ có các góc bằng nhau từng đôi một.

Phương pháp giải

Bước 1: Tính các tỉ số $\dfrac{OC}{OA}; \dfrac{OB}{OD}$

Bước 2: Xét hai tam giác OCB và OAD, chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ hai.

Hướng dẫn giải

a) Ta có:

$\dfrac{OA}{OC} = \dfrac{5}{8}$ ; $\dfrac{OD}{OB} = \dfrac{10}{16} = \dfrac{5}{8}$ 

 $\Rightarrow \dfrac{OA}{OC} = \dfrac{OD}{OB}$

Xét  $∆OCB$ và $∆OAD$ có:

+) $\widehat O$ chung

+) $\dfrac{OA}{OC} = \dfrac{OD}{OB}$ (chứng minh trên)

 $\Rightarrow ∆OCB$ đồng dạng $∆OAD$ ( c-g-c)

$\Rightarrow \widehat {ODA} = \widehat {CBO}$ (2 góc tương ứng) hay $\widehat{CDI}$ = $\widehat{IBA}$ 

b) Xét $∆ICD$ và $∆IAB$ có

 $\widehat{CID}$ = $\widehat{AIB}$ (hai góc đối đỉnh)   (1)

$\widehat{CDI}$ = $\widehat{IBA}$ (theo câu a)            (2)

Theo định lí tổng ba góc trong một tam giác ta có:

$\eqalign{ & \widehat {CID} + \widehat {CDI} + \widehat {ICD} = {180^0} \cr & \widehat {AIB}+\widehat {IBA} + \widehat {IAB} = {180^0} \cr}$

$\Rightarrow \widehat {CID} + \widehat {CDI} + \widehat {ICD}$ $= \widehat {AIB}+\widehat {IBA} + \widehat {IAB}$   (3)

Từ (1), (2) và (3) suy ra: $\widehat {ICD}=\widehat {IAB}$

Vậy hai tam giác $IAB$ và $ICD$ có các góc bằng nhau từng đôi một. 

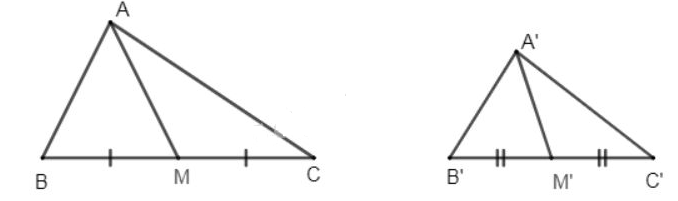
Chứng minh rằng nếu tam giác $A'B'C'$ đồng dạng với tam giác $ABC$ theo tỉ số $k$, thì tỉ số của hai đường trung tuyến tương ứng với hai tam giác đó cũng bằng $k$.

Phương pháp giải

Chứng minh hai tam giác $ABM$ và $A'B'M'$ đồng dạng.

Áp dụng:

- Định lí: Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp đó bằng nhau, thì hai tam giác đồng dạng.

- Tính chất hai tam giác đồng dạng.

Hướng dẫn giải

Giả sử $∆A'B'C'$ đồng dạng $∆ABC$ theo tỉ số $k, A'M', AM$ là hai đường trung tuyến tương ứng.

Vì $∆A'B'C'$ đồng dạng $∆ABC$ (giả thiết)

$\dfrac{A'B'}{AB} = \dfrac{B'C'}{BC}$ (tính chất hai tam giác đồng dạng)

Mà $B'C' = 2B'M', BC = 2BM$ (tính chất trung tuyến)

$\Rightarrow \dfrac{{A'B'}}{{AB}} = \dfrac{{2B'M'}}{{2BM}} = \dfrac{{B'M'}}{{BM}}$

Xét  $∆ABM$ và $∆A'B'M'$ có:

 $\widehat{B} = \widehat{B'}$ (vì $∆A'B'C'$ đồng dạng $∆ABC$) 

 $\dfrac{{A'B'}}{{AB}} = \dfrac{{B'M'}}{{BM}}$ (chứng minh trên)

$\Rightarrow ∆A'B'M'$ đồng dạng $∆ABM$ (c-g-c)

$\Rightarrow \dfrac{A'M'}{AM}= \dfrac{A'B'}{AB} = k.$

Dựng tam giác $ABC$, biết $\widehat{A}={60^o}$ và, tỉ số $\dfrac{AB}{AC} = \dfrac{4}{5}$ và đường cao $AH = 6cm$.

Phương pháp giải

Bước 1: Dựng tam giác AB'C' có cạnh AB' = 4 cm và AC' = 5 cm.

Bước 2: Dựng đường cao AH', trên đường thẳng AH' lấy điểm H sao cho AH = 6 cm.

Bước 3: Qua H kẻ đường thẳng song song với B'C' ta thu được tam giác ABC cần dựng.

Hướng dẫn giải

Cách dựng

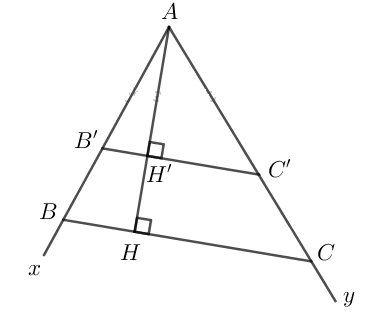
- Dựng $\widehat{xAy} = 60^o.$ Lấy trên cạnh $Ax$ điểm $B'$ sao cho $AB' = 4cm$ và trên cạnh $Ay$ lấy điểm $C'$ sao cho $AC' = 5cm.$ Ta xác định được $ΔAB'C'.$

- Dựng đường cao $AH'$ của $ΔAB'C',$ kéo dài $AH'$ và lấy trên $AH'$ một điểm $H$ sao cho $AH = 6cm.$ Từ điểm $H$ kẻ $BC // B'C'$ với $B \in Ax; \, C \in Ay.$

Chứng minh
Theo cách dựng ta có $\widehat{A} = 60^o$
Lại có: $B'C' // BC$
$\Rightarrow ΔAB'C' \backsim ΔABC$
 $\Rightarrow \dfrac{AB}{AC} = \dfrac{AB'}{AC'} = \dfrac{4}{5}$ và theo cách dựng $AH = 6cm.$