Giải bài tập SGK Toán 8 Bài 7: Trường hợp đồng dạng thứ ba

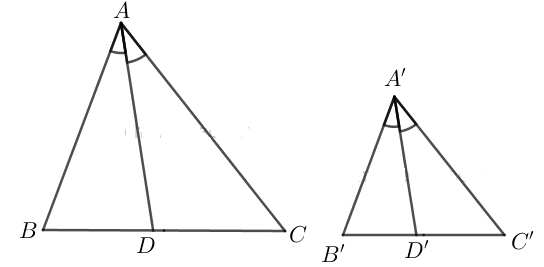
Chứng minh rằng nếu tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) theo tỉ số \(k\) thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng \(k\).

Phương pháp giải

Chứng minh hai tam giác ABD và A'B'D' đồng dạng, với D và D' là chân đường phân giác kẻ từ đỉnh A và A' của hai tam giác.

Hướng dẫn giải

Giả sử \( ΔA'B'C' \backsim ΔABC\) theo tỉ số đồng dạng \(k = \dfrac{A'B'}{AB}\) và \(AD, \, A'D'\) lần lượt là đường phân giác của \(ΔABC\) và \(ΔA'B'C'\)

Ta chứng minh \(\dfrac{A'D'}{AD} = k\)

Ta có: \(ΔA'B'C' \backsim ΔABC\)
\(\Rightarrow \widehat{B} = \widehat{B'}; \, \widehat{BAC} = \widehat{B'A'C'} \,\,\,\,(1)\)

Lại có: \(AD, \, A'D'\) lần lượt là đường phân giác của \(ΔABC\) và \(ΔA'B'C'\)
\(\Rightarrow \widehat{BAD} = \dfrac{\widehat{BAC}}{2} ; \, \widehat{B'A'D'} = \dfrac{\widehat{B'A'C'}}{2} \,\,\,\,(2)\)

Từ \((1)\) và \((2) \Rightarrow \widehat{BAD} = \widehat{B'A'D'}\)

Xét \(ΔABD\) và \(ΔA'B'D'\) có:
\( \widehat{B} = \widehat{B'}\)  (chứng minh trên)
\(\widehat{BAD} = \widehat{B'A'D'}\) (chứng minh trên)
\( \Rightarrow ΔABD \backsim ΔA'B'D'\)  (g.g)
\( \Rightarrow \dfrac{AD}{A'D'} = \dfrac{AB}{A'B'} = k\) (đpcm)

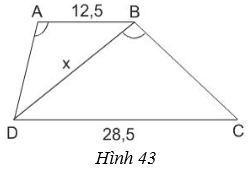
Tính độ dài \(x\) của đoạn thẳng \(BD\) trong hình 43 (Làm tròn đến chữ thập phân thứ nhất), biết rằng \(ABCD\) là hình thang (\(AB // CD\)); \(AB= 12,5cm; CD= 28,5cm\); \(\widehat{DAB} = \widehat{DBC}\).

Phương pháp giải

Chứng minh hai tam giác ABD và BDC đồng dạng, viết cặp cạnh tương ứng tỉ lệ để tính độ dài x

Hướng dẫn giải

Xét \(ΔABD\) và \(ΔBDC\) có:

\( \widehat{A} = \widehat{B}\)  (giả thiết)

\(\widehat{ABD} = \widehat{BDC}\)  (vì \(AB // CD\))

\( \Rightarrow ΔABD \backsim ΔBDC\) (g.g)

\( \Rightarrow \dfrac{AB}{BD} = \dfrac{BD}{DC}\) (cặp cạnh tương ứng tỉ lệ)

Hay \(\dfrac{12,5}{x} = \dfrac{x}{28,5}\)

\( \Rightarrow x^2 = 12,5.28,5 = 356,25\)

\( \Rightarrow x = 18,874 \, (cm) \, \approx 18,9 \,(cm)\)

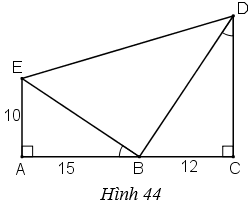
Hình 44 cho biết \(\widehat{EBA} = \widehat{BDC} \)

a) Trong hình vẽ có bao nhiêu tam giác vuông? Hãy kể tên các tam giác đó.

b) Cho biết \(AE = 10cm,\, AB = 15cm,\, BC = 12cm.\) Hãy tính độ dài các đoạn thẳng \(CD,\, BE,\, BD\) và \(ED\) (làm tròn đến chữ số thập phân thứ nhất).

c) So sánh diện tích tam giác \(BDE\) với tổng diện tích của hai tam giác \(AEB\) và \(BCD.\)

Phương pháp giải

a) Tam giác có 1 góc vuông là tam giác vuông.

b) Sử dụng định lý Pi -ta -go để tính độ dài các đoạn thẳng và cạnh tương ứng tỉ lệ của hai tam giác đồng dạng để tính độ dài các đoạn thẳng.

c) Sử dụng: Công thức tính diện tích tam giác, diện tích hình thang.

Hướng dẫn giải

a) Ta có: \(\widehat{EBA} = \widehat{BDC}\) (giả thiết) mà \(\widehat{BDC} + \widehat{CBD}={90^0}\) (do tam giác BCD vuông tại C) 

\( \Rightarrow \widehat{EBA} + \widehat{CBD}={90^0}\) 

Vậy \(\widehat{EBD} = {180^0} - (\widehat{EBA}+ \widehat{CBD})\)\(\, = {180^o} - {90^o} = {90^o}\)

Vậy trong hình vẽ có ba tam giác vuông đó là:

\(∆ABE, ∆CBD, ∆EBD.\) 

b) \(∆ABE\) và \(∆CDB\) có:

\(\widehat{A} = \widehat{C}=90^o\)

\(\widehat{ABE}= \widehat{CDB}\) (giả thiết)

\( \Rightarrow  ∆ABE ∽ ∆CDB\) (g-g)

\( \Rightarrow \dfrac{AB}{CD} = \dfrac{AE}{CB}\) (tính chất hai tam giác đồng dạng)

\( \Rightarrow CD = \dfrac{AB.CB}{AE} = 18\, (cm)\)

- Áp dụng định lí pitago ta có:

\( ∆ABE\) vuông tại \(A\)

\( \Rightarrow  BE = \sqrt{AE^{2}+AB^{2}}\) \(\,=\sqrt{10^{2}+15^{2}}\) \( \approx  18\, (cm)\).

 \(∆BCD\) vuông tại \(C\)

\( \Rightarrow BD = \sqrt {B{C^2} + D{C^2}}  \) \(= \sqrt {{{12}^2} + {{18}^2}}  \approx 21,6\,\,cm\)

\(∆EBD\) vuông tại \(B\)

\( \Rightarrow  ED = \sqrt{EB^{2}+BD^{2}}\) \(=\sqrt{325+ 468} \approx 28,2\, (cm)\)

c) Ta có: 

\(S_{ABE} + S_{DBC}\)

\(= \dfrac{1}{2}AE.AB + \dfrac{1}{2}BC.CD\) 

\(= \dfrac{1}{2}. 10.15 + \dfrac{1}{2}.12.18\)

\(= 75 + 108 = 183\;cm^2\).

Ta có: \(A{\rm{E}}//DC\,\,\left(\text{ cùng } { \bot AC} \right) \Rightarrow \) \(ACDE\) là hình thang.

\(S_{ACDE} = \dfrac{1}{2}.(AE + CD).AC\)

\(= \dfrac{1}{2}.(10 + 18).27= 378\;cm^2\)

\( \Rightarrow S_{EBD} = S_{ACDE} - (S_{ABE}+ S_{DBC})\)\(\; = 378 - 183 = 195\,cm^2\)

\(S_{EBD}> S_{ABE} + S_{DBC}\) \(( 195 > 183)\).