Giải bài tập SGK Toán 8 Ôn tập chương 3: Tam giác đồng dạng

Xác định tỉ số của hai đoạn thẳng \(AB\) và \(CD\) trong các trường hợp sau:

a) \(AB = 5cm,\, CD = 15cm\)

b) \(AB = 45dm;\, CD = 150cm\)

c) \(AB = 5CD\)

Phương pháp giải

Tỉ số của hai đoạn thẳng \(AB\) và \(DC\) là tỉ số độ dài cùng đơn vị đo của hai đoạn thẳng đó

Hướng dẫn giải

a) \(AB  = 5cm\) và \(CD = 15cm\)

\( \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{5}{{15}} = \dfrac{1}{3}\)

b) \(AB = 45dm = 450cm\) và \(CD = 150 cm\)

\( \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{{450}}{{150}} = 3\)

c) \(AB = 5CD\) \( \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{{5CD}}{{CD}} = 5\)

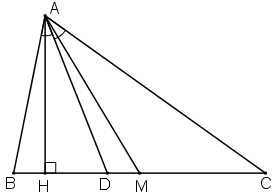
Cho tam giác \(ABC (AB < AC)\). Vẽ đường cao \(AH\), đường phân giác \(AD\), đường trung tuyến \(AM\). Có nhận xét gì về vị trí của ba điểm \(H, D, M\).

Phương pháp giải

Áp dụng: Tính chất đường phân giác của tam giác, quan hệ giữa cạnh và góc trong tam giác chứng minh:

Bước 1: \(M \) nằm giữa \(D\) và \(C\)

Bước 2: \(D\) nằm giữa hai điểm \(H\) và \(C\)

Bước 3: Kết luận: \(D\) nằm giữa \(H\) và \(M.\)

Hướng dẫn giải

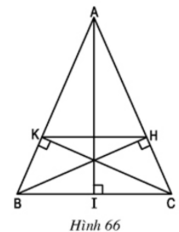
Cho tam giác cân \(ABC (AB = AC)\), vẽ các đường cao \(BH, CK\) (H.66).

Phương pháp giải

a) Chứng minh hai tam giác vuông \(BKC\) và \(CHB\) bằng nhau.

b) Sử dụng định lí Ta lét đảo chứng minh: \(\dfrac{{AK}}{{AB}} = \dfrac{{AH}}{{AC}}\)

c) Vẽ thêm đường cao \(AI\), xét hai tam giác đồng dạng \(IAC\) và \(HBC\) rồi tính \(CH\).

Tiếp theo, xét hai tam giác đồng dạng \(AKH\) và \(ABC\) rồi tính \(HK\).

Hướng dẫn giải

a) Xét hai tam giác vuông \(BKC\) và \(CHB\) có:

\(\widehat {KBC} = \widehat {HCB}\) (\(∆ABC\) cân tại \(A\))

\(BC\) là cạnh chung 

\( \Rightarrow ∆BKC = ∆CHB\) (cạnh huyền - góc nhọn)

\( \Rightarrow BK = CH\) (2 cạnh tương ứng)

b) Ta có : \(AK = AB - BK, AH = AC - HC\) (gt)

Mà \(AB = AC\) (\(∆ABC\) cân tại \(A\))

\(BK = CH\) (chứng minh trên) 

\( \Rightarrow  AK = AH\)

Do đó : \(\dfrac{{AK}}{{AB}} = \dfrac{{AH}}{{AC}}\) \( \Rightarrow KH // BC\) (định lí Ta lét đảo)

c) \(BH\) cắt \(CK\) tại \(M \Rightarrow M\) là trực tâm của \(∆ABC\) (định nghĩa trực tâm)

\(\Rightarrow AM ⊥ BC\) tại \(I\) (tính chất trực tâm)

Xét \(∆AIC\) và \(∆BHC\) có:

\(\widehat{I} = \widehat{H } = 90^o\)

\(\widehat{C}\) chung

\(\Rightarrow ∆AIC \backsim ∆BHC\) (g - g)

\(\Rightarrow \dfrac{IC}{HC} = \dfrac{AC}{BC}\) (tính chất hai tam giác đồng dạng)

\(\Rightarrow \dfrac{\dfrac{a}{2}}{HC} = \dfrac{b}{a}\\ \Rightarrow HC = \dfrac{BC.AH}{AC}\\ \Rightarrow HK = \dfrac{a}{b}. \dfrac{2b^2 - a^2}{2b} = \dfrac{2ab^2 - a^3}{2b^2} = a - \dfrac{a^3}{2b^2}\)

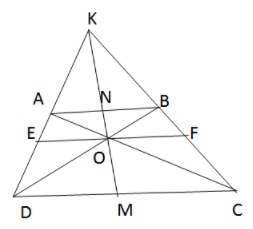
Hình thang \(ABCD \,(AB//CD)\) có \(AC\) và \(BD\) cắt nhau tại \(O, AD\) và \(BC\) cắt nhau tại \(K\). Chứng minh rằng \(OK\) đi qua trung điểm của các cạnh \(AB\) và \(CD\).

Phương pháp giải

- Qua \(O\) kẻ đường thẳng song song với \(AB, CD\) cắt \(AD, BC\) lần lượt tại \(E, F\).

- Chứng minh \(\dfrac{{AN}}{{EO}}=\dfrac{{BN}}{{FO}}\).

- Chứng minh \(\dfrac{{EO}}{{DM}}=\dfrac{{FO}}{{CM}}\).

Hướng dẫn giải

Qua \(O\) kẻ đường thẳng song song với \(AB, CD\) cắt \(AD, BC\) lần lượt tại \(E, F\).

Suy ra \(AB//EF//CD\)

Gọi N là giao của KO và AB, M là giao của KO với DC.

Ta có: \(OE // DC\) (gt) 

\( \Rightarrow \dfrac{{OE}}{{DC}} = \dfrac{{AO}}{{AC}}\left( 1 \right)\) (hệ quả của định lí TaLet)

\(OF // DC\) (gt)

\( \Rightarrow \dfrac{{OF}}{{DC}} = \dfrac{{BF}}{{BC}}\left( 2 \right)\) (hệ quả của định lí TaLet)

\(OF // AB\) (gt)

\( \Rightarrow \dfrac{{BF}}{{BC}} = \dfrac{{OA}}{{AC}}\) (3) (hệ quả của định lí TaLet)

Từ (1), (2) và (3) ta có: 

\(\dfrac{{OE}}{{DC}} = \dfrac{{OF}}{{DC}} \Rightarrow OE = OF\)

Ta có: \(AB//EF\) (gt) áp dụng hệ quả của định lí TaLet ta có: 

\(\begin{array}{l}
\Rightarrow \dfrac{{AN}}{{EO}} = \dfrac{{KN}}{{K{\rm{O}}}};\,\dfrac{{BN}}{{F{\rm{O}}}} = \dfrac{{KN}}{{K{\rm{O}}}}\\
\Rightarrow \dfrac{{AN}}{{EO}} = \dfrac{{BN}}{{F{\rm{O}}}} \\\text{Mà  } EO=FO\\ \Rightarrow AN = BN
\end{array}\)

\( \Rightarrow \) \(N\) là trung điểm của \(AB.\)

Tương tự ta có: \(EF // DC\) (gt) áp dụng hệ quả của định lí TaLet ta có:

\(\begin{array}{l}
\Rightarrow \dfrac{{EO}}{{DM}} = \dfrac{{KO}}{{K{\rm{M}}}};\,\dfrac{{FO}}{{C{\rm{M}}}} = \dfrac{{KO}}{{K{\rm{M}}}}\\
\Rightarrow \dfrac{{EO}}{{DM}} = \dfrac{{FO}}{{C{\rm{M}}}}\\\text{Mà  }EO=FO\\ \Rightarrow DM = CM
\end{array}\)

\( \Rightarrow M\) là trung điểm của \(CD\).

Vậy \(OK\) đi qua trung điểm của các cạnh \(AB\) và \(CD\). 

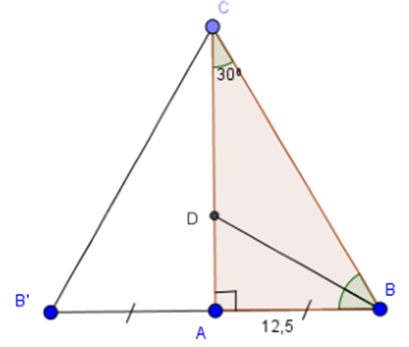
Cho tam giác vuông \(ABC\), \(\widehat A =90^0, \widehat C=30^0\) và đường phân giác \(BD\) (\(D\) thuộc cạnh \(AC\)). 

a) Tính tỉ số \(\dfrac{{A{\rm{D}}}}{{C{\rm{D}}}}\) .

b) Cho biết độ dài \(AB = 12,5 cm\). Hãy tính chu vi và diện tích của tam giác \(ABC\).

Phương pháp giải

Áp dụng: Tính chất đường phân giác của tam giác, định lí Pitago, công thức tính chu vi và diện tích của tam giác.

a) Muốn tính tỉ số \(\dfrac{{A{\rm{D}}}}{{C{\rm{D}}}}\) ta cần chứng minh \(\dfrac{{AB}}{{BC}} =\dfrac{{AB}}{{BB'}}= \dfrac{1}{2}\)

b) Xét tam giác \(ABC\)

- Chu vi tam giác là: \(p = AB + BC + CA\)

- Diện tích tam giác là: \({S_{ABC}} = \dfrac{1 }{ 2}AB.AC\)

Hướng dẫn giải

a) Xét tam giác \(BCA\) vuông tại \(A\) (gt) có: 

\(\begin{array}{l}
\widehat {ACB} + \widehat {ABC} = {90^0}\\
\Rightarrow \widehat {ABC} = {90^0} - \widehat {ACB} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;= {90^0} - {30^0} = {60^0}
\end{array}\)

Trên tia đối của tia \(AB\) lấy điểm \(B'\) sao cho \(AB = AB'\) (1)

Xét hai tam giác vuông \(ABC\) và \(AB'C\) có:

\(AC\) chung (gt)

\(AB = AB'\) (gt)

\( \Rightarrow \Delta ABC = \Delta AB'C\) (cạnh góc vuông - cạnh góc vuông)

\( \Rightarrow BC = B'C\) (2 cạnh tương ứng)

\( \Rightarrow \Delta BB'C\) cân tại \(C\).

Lại có \(\widehat {ABC} = {60^0}\) nên suy ra \(\Delta BB'C\) đều (dấu hiệu nhận biết tam giác đều) (2)

Từ (1) và (2) \( \Rightarrow \dfrac{{AB}}{{BC}} =\dfrac{{AB}}{{BB'}}= \dfrac{1}{2}\)

Vì \(BD\) là đường phân giác của \(\Delta ABC\) nên:

\(\dfrac{{DA}}{{DC}} = \dfrac{{BA}}{{BC}} = \dfrac{1}{2}\)

b) \(∆ABC\) vuông tại \(A\) nên áp dụng định lí Pitago ta có:

\(\eqalign{
& A{C^2} = B{C^2} - A{B^2},\,BC = 2AB \cr
& \Rightarrow A{C^2} = 4A{B^2} - A{B^2} = 3A{B^2} \cr
& \Rightarrow AC = \sqrt {3A{B^2}} = AB\sqrt 3 \cr
& = 12,5\sqrt 3 \approx 21,65\,cm \cr} \)

Gọi \(p\) là chu vi \(∆ABC\)

\( \Rightarrow p = AB + BC + CA\)

\( \Rightarrow p = 3AB + AC = 3.12,5 + 12,5\sqrt 3 \)

\( \Rightarrow p = 12,5 (3+\sqrt 3 ) \approx 59,15\left( {cm} \right)\)

\({S_{ABC}} = \dfrac{1 }{ 2}AB.AC \approx 135,31(c{m^2})\)

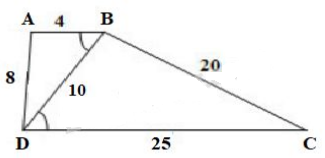
Tứ giác \(ABCD\) có \(AB = 4cm, BC = 20 cm\), \(CD = 25 cm, DA = 8cm\), đường chéo \(BD = 10cm\).

a) Nêu cách vẽ tứ giác \(ABCD\) có kích thước đã cho ở trên.

b) Các tam giác \(ABD\) và \(BDC\) có đồng dạng với nhau không? Vì sao?

c) Chứng minh rằng \(AB // CD\).

Phương pháp giải

Áp dụng cách vẽ tam giác, dấu hiệu nhận biết hình thang, dấu hiệu nhận biết hai tam giác đồng dạng.

Hướng dẫn giải

a) Cách vẽ:

- Vẽ \(ΔBDC\):

+ Vẽ \(DC = 25cm\)

+ Vẽ cung tròn tâm \(D\) có bán kính \(10cm\) và cung tròn tâm \(C\) có bán kính \(20cm\). Giao điểm của hai cung tròn là \( B\).

- Vẽ điểm A: Vẽ cung tròn tâm \(B\) có bán kính \( 4cm\) và cung tròn tâm \(D\) có bán kính \( 8cm\). Giao điểm của hai cung tròn này là điểm \(A\). Nối các cạnh BD, BC, DA, BA. 

Vậy là ta đã vẽ được tứ giác \(ABCD\) thỏa mãn điều kiện đề bài.

b) Ta có: \(\dfrac{{AB}}{{BD}} = \dfrac{4}{{10}} = \dfrac{2}{5};\) \(\dfrac{{BD}}{{DC}} = \dfrac{{10}}{{25}} = \dfrac{2}{5};\) \(\dfrac{{AD}}{{BC}} = \dfrac{8}{{20}} = \dfrac{2}{5}\)

\( \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}} = \dfrac{{AD}}{{BC}}\)

\(\Rightarrow \Delta AB{\rm{D}} \backsim \Delta B{\rm{D}}C\left( {c - c - c} \right)\)

c) \(∆ABD∽ ∆BDC\) (chứng minh trên)

\(\Rightarrow \widehat {ABD} = \widehat {BDC}\), mà hai góc ở vị trí so le trong.

\(\Rightarrow AB // DC\) hay \(ABCD\) là hình thang.