Giải bài tập SGK Toán 8 Bài 2: Tính chất cơ bản của phân thức

Cô giáo yêu cầu mỗi bạn cho một ví dụ về hai phân thức đại số bằng nhau. Dưới đây là những ví dụ các bạn Lan, Hùng, Hương, Huy đã cho:

a) \( \dfrac{x + 3}{2x - 5} = \dfrac{x^{2}+ 3x}{2x^{2} - 5x}\) ( Lan)

b) \( \dfrac{(x + 1)^{2}}{x^{2} + x} = \dfrac{x + 1}{1}\) ( Hùng)

c) \( \dfrac{4 - x}{-3x} = \dfrac{x - 4}{3x}\) ( Giang)

d) \( \dfrac{(x - 9)^{3}}{2(9 - x)}= \dfrac{(9 - x)^{2}}{2}\) ( Huy)

Em hãy dùng tính chất cơ bản của phân thức và qui tắc đổi dấu để giải thích ai viết đúng, ai viết sai. Nếu có chỗ nào sai em hãy sửa lại cho đúng.

Phương pháp giải

Áp dụng tính chất cơ bản của phân thức và quy tắc đổi dấu phân thức:

- Nếu nhân (hoặc chia) cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

- Nếu đổi dấu cả tử và mẫu của một phân thức thì được một phân thức mới bằng phân thức đã cho.

Hướng dẫn giải

Câu a: \( \dfrac{x + 3}{2x - 5}= \dfrac{x(x + 3)}{(2x - 5)x}= \dfrac{x^{2} + 3x}{2x^{2}- 5x}\) Lan viết đúng

Câu b: \( \dfrac{(x + 1)^{2}}{x^{2}+ x}= \dfrac{(x + 1)^{2}}{x(x + 1)}\)

\(=\dfrac{{{{(x + 1)}^2}:\left( {x + 1} \right)}}{{x(x + 1):\left( {x + 1} \right)}}= \dfrac{x + 1}{x}\) 

Hùng viết sai vì đã chia tử của vế trái cho nhân tử chung \(x + 1\) thì cũng phải chia mẫu của nó cho \(x + 1\). Sửa lại là:

\( \dfrac{(x + 1)^{2}}{x^{2}+ x}= \dfrac{x + 1}{x}\) hoặc \( \dfrac{(x + 1)^{2}}{x + 1}= \dfrac{x + 1}{1}\)

Câu c: \( \dfrac{4 - x}{-3x}= \dfrac{-(4 - x)}{-(-3x)}= \dfrac{x - 4}{3x}\) Giang viết đúng

Câu d: \((x - 9)^3= (-(9 - x))^3= -(9 - x)^3\)

Do đó:

\( \dfrac{(x - 9)^{3}}{2(9 - x)} = \dfrac{-(9 - x)^{3}}{2(9 - x)}\)

\(= \dfrac{{ - {{(9 - x)}^3}:\left( {9 - x} \right)}}{{2(9 - x):\left( {9 - x} \right)}}= \dfrac{-(9 - x)^{2}}{2}\)

Suy ra Huy viết sai.

 Sửa lại: \( \dfrac{(x - 9)^{3}}{2(9 - x)} = \dfrac{-(9 - x)^{2}}{2}\) hoặc \( \dfrac{(x - 9)^{3}}{2(9 - x)} = \dfrac{(9 - x)^{2}}{-2}\) hoặc \( \dfrac{(9 - x)^{3}}{2(9 - x)}= \dfrac{(9 - x)^{2}}{2}\)

Điền đa thức thích hợp vào mỗi chỗ trống trong các đa thức sau:

a) \(\dfrac{x^3 + x^2}{(x - 1)(x + 1)} = \dfrac{...}{x - 1}\)

b) \(\dfrac{5(x + y)}{2} = \dfrac{5x^2 - 5y^2}{...}\)

Phương pháp giải

Áp dụng tính chất cơ bản của phân thức: Nếu nhân (hoặc chia) cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

Hướng dẫn giải

Câu a

Ta có: \( \dfrac{x^{3} + x^{2}}{(x - 1)(x + 1)}= \dfrac{x^{2}(x + 1)}{(x - 1)(x + 1)}\)

Chia cả tử và mẫu cho \((x+1)\), ta được:

\(\dfrac{x^{2}(x + 1)}{(x - 1)(x + 1)}\)\(= \dfrac{x^{2}(x + 1):(x+1)}{(x - 1)(x + 1):(x+1)}= \dfrac{x^{2}}{x - 1}.\)

Vậy phải điền  \(x^2\) vào chỗ trống.

Câu b

Phân tích tử của phân thức ở vế phải ta được \(5{x^2} - 5{y^2} =5(x^2-y^2)\)\(= 5\left( {x + y} \right)\left( {x - y} \right)\). Do đó đẳng thức đã cho có thể viết là: 

\(\dfrac{{5\left( {x + y} \right)}}{2} = \dfrac{{5\left( {x + y} \right)\left( {x - y} \right)}}{...}\)

Như vậy ta phải nhân cả tử và mẫu của phân thức ở vế trái với \((x-y),\) ta được:

\(\dfrac{{5\left( {x + y} \right)}}{2} = \dfrac{{5\left( {x + y} \right)\left( {x - y} \right)}}{2(x-y)}\)\(= \dfrac{{5{{\rm{x}}^2} - 5{y^2}}}{{2(x - y)}}\)

Vậy đa thức phải điền vào chỗ trống là \(2(x-y)\).

Đố. Hãy dùng tính chất cơ bản của phân thức để điền một đa thức thích hợp vào chỗ trống:

\(\dfrac{x^5 - 1}{x^2 - 1} = \dfrac{...}{x + 1}\)

Phương pháp giải

Áp dụng tính chất cơ bản của phân thức và áp dụng hằng đẳng thức hiệu hai bình phương, phép chia đa thức một biến đã sắp xếp.

Hướng dẫn giải

Ta có: \(x^2-1=(x-1)(x+1)\)

Vế phải chứng tỏ đã chia mẫu của vế trái cho \(x - 1\)

Vậy phải chia tử của vế trái \(x^5– 1\) cho \(x - 1\)

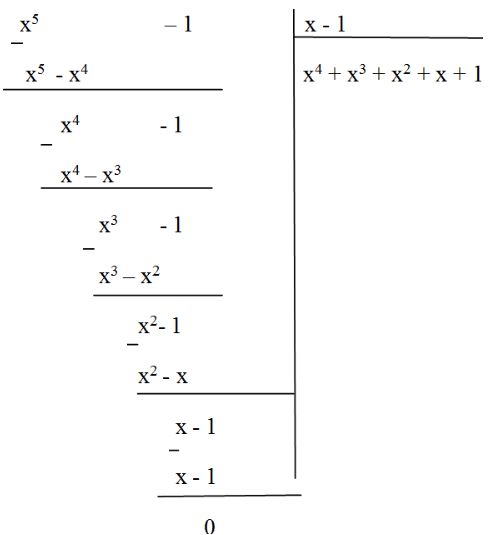
Suy ra \(x^5-1=({x^4} + {x^3} + {x^2} + x + 1)(x-1)\)

Ta có:

\( \dfrac{x^{5}- 1}{x^{2}- 1}= \dfrac{({x^4} + {x^3} + {x^2} + x + 1)(x-1)}{(x + 1)(x-1)}\)

\(= \dfrac{({x^4} + {x^3} + {x^2} + x + 1)(x-1):(x-1)}{(x + 1)(x-1):(x-1)}\)

\(= \dfrac{{x^4} + {x^3} + {x^2} + x + 1}{x + 1}\)

Vậy phải điền vào chỗ trống: \({x^4} + {x^3} + {x^2} + x + 1\)