Giải bài tập SGK Toán 8 Bài: Luyện tập

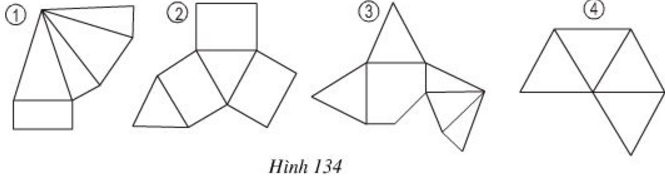
Trong các miếng bìa ở hình 134, miếng nào khi gấp và dán lại thì được một hình chóp đều?

Phương pháp giải

Dựa vào định nghĩa và tính chất của hình chóp đều.

Hình chóp đều là hình chóp có mặt đáy là một đa giác đều, có mặt bên là những tam giác cân bằng nhau có chung đỉnh.

Hướng dẫn giải

Hình 1: Khi gấp lại không được hình chóp đều vì hình chóp thu được có đáy là hình chữ nhật. Không là đa giác đều.

Hình 2: Khi gấp lại ta được hình lăng trụ đứng đáy tam giác đều, không phải là hình chóp tam giác đều.

Hình 3: Khi gấp lại không được hình chóp tam giác đều vì hình chóp thu được có được đáy là hình ngũ giác không phải là ngũ giác đều.

Hình 4: Khi gấp lại không được hình chóp đều vì hình thu được là hình chóp đều thiếu một mặt đáy và dư một mặt bên.

Tính diện tích toàn phần của:

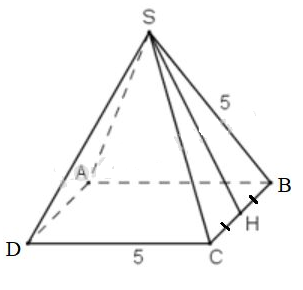
a) Hình chóp tứ giác đều, biết cạnh đáy \(a = 5cm,\) cạnh bên \(b = 5cm;\,\sqrt{18,75} ≈ 4,33;\)

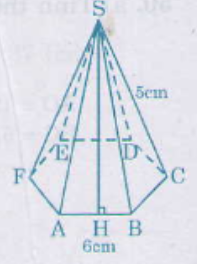
b) Hình chóp lục giác đều, biết cạnh đáy \(a = 6cm,\) cạnh bên \(b = 10cm;\, \sqrt{3} ≈ 1,73;\, \sqrt{91} ≈9,54.\)

Phương pháp giải

Áp dụng các công thức : 

\(S_{tp} = S_{xq} +S{đ}\) 

\(S_{xq} = p.d \), trong đó \(p \) là nửa chu vi đáy, \( d\) là trung đoạn của hình chóp.

Hướng dẫn giải

a) 

Từ đề bài ta có các mặt bên của hình chóp đều là những tam giác đều cạnh \(5cm\).

Đường cao của mỗi mặt bên là: 

 \(d=SH = \sqrt{SC^{2} -HC^{2}}\)

 \(= \sqrt{5^{2} -2,5^{2}}= \sqrt{18,75}\approx 4,33 (cm) \)

Diện tích xung quanh hình chóp là:

\(S_{xq} = p.d = \dfrac{1}{2}. 5.4.4,33 = 43,3 (cm^2) \) 

Diện tích đáy hình chóp:

\(S_{đ} = a^2 = 5^2 =25(cm^2) \)

Diện tích toàn phần hình chóp:

\( S_{tp} = S_{xq}+ S_{đ} = 43,3 + 25 = 68,3 \) \((cm^2)\)

b) 

Mặt bên của hình chóp lục giác đều là tam giác cân có cạnh bên \(10cm\), cạnh đáy \(6cm\) .

Đường cao \(SH\) của mặt bên là: 

\(d=SH = \sqrt{SA^{2} -AH^{2}} = \sqrt{10^{2} -3^{2}} \) \(= \sqrt{91}\approx   9,54 (cm) \) 

Diện tích xung quanh hình chóp:

\(S_{xq} = p.d = \dfrac{1}{2}. 6.6.9,54 = 171,72\) \( (cm^2) \) 

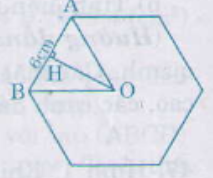
Đáy của hình chóp là lục giác đều. Diện tích lục giác bằng \(6\) lần diện tích tam giác đều \(ABO\).

Chiều cao của tam giác đều OAB là:

 \(OH = \sqrt{OB^{2} -BH^{2}} = \sqrt{6^{2} -3^{2}}\) \(= \sqrt{27}\approx  5,2 (cm) \) 

Diện tích đáy hình chóp:

\(S_{đ} =6.\dfrac{1}{2}.OH.AB=6. \dfrac{1}{2}5,2.6 = 93,6(cm^2) \)

Diện tích toàn phần hình chóp: 

\( S_{tp} = S_{xq}+ S_{đ} = 171,72 + 93,6 \) \(= 265,32 (cm^2)\)

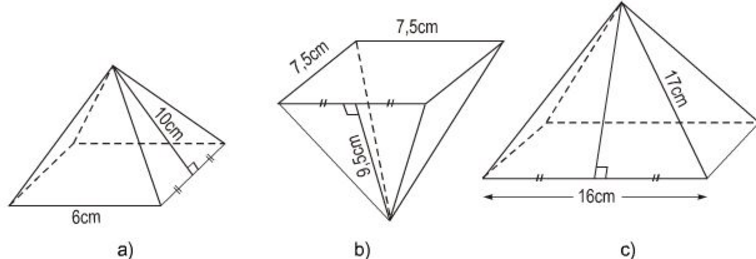
Tính diện tích xung quanh của các hình chóp tứ giác đều sau đây (h.135):

Phương pháp giải

Tính diện tích xung quanh theo công thức: \(S_{xq} = p.d\), trong đó \(p\) là nửa chu vi đáy, \(d\) là trung đoạn của hình chóp đều.

Hướng dẫn giải

Hình a

Diện tích xung quanh của hình chóp là: 

\(S_{xq} = p.d =  \dfrac{1}{2}. 6.4.10 = 120 (cm^2)\)

Hình b

Diện tích xung quanh của hình chóp là:  

\(S_{xq} = p.d =  \dfrac{1}{2}. 7,5.4.9,5 = 142,5\) \( (cm^2)\)

Hình c

Độ dài trung đoạn của hình chóp là :

\(d = \sqrt{17^{2} -8^{2}} = \sqrt{289 -64}= \sqrt{225} \) \(= 15(cm) \) 

Diện tích xung quanh của hình chóp là: 

\(S_{xq} = p.d =  \dfrac{1}{2}. 16.4.15 = 480 (cm^2)\)

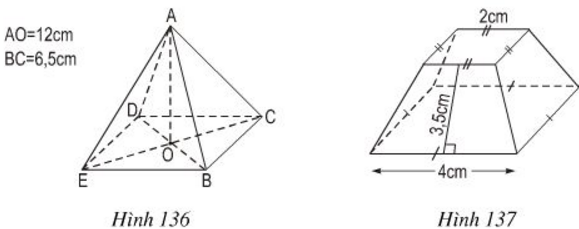
a) Tính thể tích của hình chóp đều (h.136).

b) Tính diện tích xung quanh của hình chóp cụt đều (h.137).

(Hướng dẫn: Diện tích cần tính bằng tổng diện tích các mặt xung quanh. Các mặt xung quanh là những hình thang cân với cùng chiều cao, các cạnh đáy tương ứng bằng nhau, các cạnh bên bằng nhau)

Phương pháp giải

a) Tính thể tích hình chóp theo công thức: \(V = \dfrac{1}{3} .S.h\), trong đó \(S\) là diện tích đáy, \(h\) là chiều cao. 

b) Tính diện tích hình thang theo công thức: \(S = \dfrac{(a+b). h}{2} \), trong đó \(a,\; b\) là là hai đáy của hình thang, \(h\) là chiều cao.

Hướng dẫn giải

a) Diện tích đáy của hình chóp đều: 

\( S = BC^2 = 6,5^2 = 42,25 (cm^2)\)

Thể tích hình chóp đều là:

\( V = \dfrac{1}{3} .S.h = \dfrac{1}{3} . 42,25 .12 =  169\)\(\, (cm^3)\)

b) Các mặt xung quanh là những hình thang cân đáy nhỏ \(2cm\), đáy lớn \(4cm\) , chiều cao \(3,5cm\).

Diện tích xung quanh của hình chóp cụt đều là:

\(S_{xq} = 4. \dfrac{(2+4). 3,5}{2} =42 (cm^2) \)