Giải bài tập SGK Toán 8 Bài: Luyện tập 1

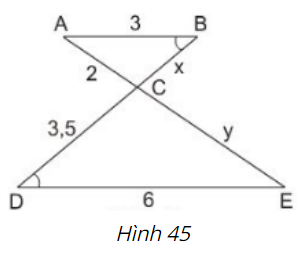
Tính độ dài \(x,\, y\) của các đoạn thẳng trong hình 45.

Phương pháp giải

Giải bài toán bằng cách chứng minh hai tam giác ABC và EDC đồng dạng với nhau.

Hướng dẫn giải

Ta có: \(\widehat{ABD}\) = \(\widehat{BDE}\) (gt) mà hai góc ở vị trí so le trong

\( \Rightarrow AB // DE\) (dấu hiệu nhận biết hai đường thẳng song song)

Áp dụng định lí:Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

\( \Rightarrow  ∆ABC ∽ ∆EDC \)

\( \Rightarrow \dfrac{AB}{ED} = \dfrac{BC}{DC} = \dfrac{AC}{EC}\) (tính chất hai tam giác đồng dạng)

\(\Rightarrow \dfrac{3}{6} = \dfrac{x}{3,5} =  \dfrac{2}{y}\)

\( \Rightarrow x = \dfrac{3. 3,5}{6} = 1,75\); 

\( \Rightarrow y = \dfrac{6.2}{3} = 4\)

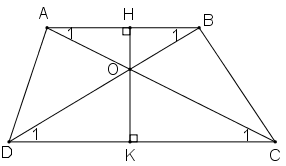
Cho hình thang \(ABCD (AB//CD)\). Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\).

a) Chứng minh rằng \(OA.OD = OB.OC\). 

b) Đường thẳng qua \(O\) vuông góc với \(AB\) và \(CD\) theo thứ tự tại \(H\) và \(K\).

Chứng minh rằng \(\dfrac{OH}{OK} = \dfrac{AB}{CD}\)

Phương pháp giải

a) Chứng minh \( \dfrac{OA}{OC} = \dfrac{OB}{OD}\) bằng cách chỉ ra tam giác OAB đồng dạng với tam giác OCD.

b) Chứng minh \( ΔOAH \backsim ΔOCK\)

Hướng dẫn giải

a) Vì \(AB // CD\) (giả thiết)

Áp dụng định lí:Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

\( \Rightarrow ∆AOB ∽ ∆COD\) 

\( \Rightarrow \dfrac{OA}{OC} = \dfrac{OB}{OD}\) (tính chất hai tam giác đồng dạng)

\( \Rightarrow  OA.OD = OC.OB\)

b) Theo câu a) ta có \( ∆AOB ∽ ∆COD\) nên \(\dfrac{OA}{OC} = \dfrac{AB}{CD}\)  (1)

Xét \(∆AOH\) và \(∆COK\) có:

\(\widehat{AHO} = \widehat{CKO} = {90^o}\)

\(\widehat {HOA} = \widehat {K{\rm{O}}C}\) (đối đỉnh)

\( \Rightarrow ∆AOH ∽ ∆COK\) (g-g)

\( \Rightarrow \dfrac{OH}{OK}= \dfrac{OA}{OC}\)  (2) (tính chất hai tam giác đồng dạng)

Từ (1) và (2) \( \Rightarrow \dfrac{OH}{OK} = \dfrac{AB}{CD}\)

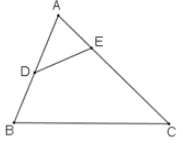
Cho tam giác \(ABC\), trong đó \(AB = 15cm, AC = 20cm\). Trên hai cạnh \(AB\) và \(AC\) lần lượt lấy điểm \(D\) và \(E\) sao cho \(AD = 8cm, AE = 6cm\). Hai tam giác \(ABC\) và \(ADE\) có đồng dạng với nhau không? Vì sao?

Phương pháp giải

Áp dụng: Định lí: Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp đó bằng nhau, thì hai tam giác đồng dạng.

Hướng dẫn giải

Ta có: \(\dfrac{AE}{AD} = \dfrac{6}{8} = \dfrac{3}{4}\); \(\dfrac{AB}{AC} = \dfrac{15}{20} = \dfrac{3}{4}\)

\( \Rightarrow  \dfrac{AE}{AD} = \dfrac{AB}{AC}\)

Xét \(∆AED\) và \(∆ABC\) có:

+) \(\dfrac{AE}{AD} = \dfrac{AB}{AC}\) (chứng minh trên)

+) \(\widehat{A}\) chung 

\( \Rightarrow  ∆AED ∽ ∆ABC\) (c-g-c)